【题目】如图,已知抛物线![]() :
: ![]() 与圆
与圆![]() :
: ![]() (
(![]() )相交于
)相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点.
四个点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)当四边形![]() 的面积最大时,求对角线
的面积最大时,求对角线![]() 、
、![]() 的交点
的交点![]() 的坐标.
的坐标.

参考答案:
【答案】(1) (2)
(2)![]()
【解析】(Ⅰ)将抛物线![]() 代入圆
代入圆![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .............(1)
.............(1)
抛物线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴![]()
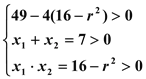 即{
即{
![]() 解这个不等式组得
解这个不等式组得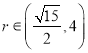 .
.
(II) 设四个交点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() 。则直线AC、BD的方程分别为
。则直线AC、BD的方程分别为
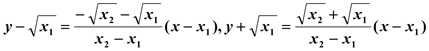
解得点P的坐标为![]() 。则由(I)根据韦达定理有
。则由(I)根据韦达定理有![]() ,
,  由于四边形ABCD为等腰梯形,因而其面积
由于四边形ABCD为等腰梯形,因而其面积![]()
![]()
令![]() ,则
,则![]() 下面求
下面求![]() 的最大值。
的最大值。
方法1:由三次均值有:
![]()
![]()
当且仅当![]() ,即
,即![]() 时取最大值。经检验此时
时取最大值。经检验此时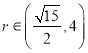 满足题意。故所求的点P的坐标为
满足题意。故所求的点P的坐标为![]()
法2:令![]() ,
,![]() ,
,
∴![]() ,
,
令![]() 得
得![]() ,或
,或![]() (舍去)
(舍去)
当![]() 时,
时,![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时,
时,![]()
故当且仅当![]() 时,
时,![]() 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线
 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;(2)已知与直线
 平行的直线
平行的直线 过点
过点 ,且与曲线
,且与曲线 交于
交于 两点,试求
两点,试求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数y=f(x),当x≥0时,f(x)=x2﹣2x.
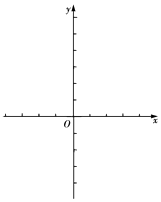
(1)求当x<0时,函数y=f(x)的解析式,并在给定坐标系下,画出函数y=f(x)的图象;
(2)写出函数y=|f(x)|的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,
 ,
, =4 ,
=4 , ,F为棱AE的中点.
,F为棱AE的中点.
(1)求证:平面
 平面
平面 ;
;(2)若直线
 与平面
与平面 所成角为
所成角为 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)试判断f (x)的单调性,并证明你的结论;
(2)若f (x)为定义域上的奇函数,求函数f (x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.例如函数
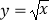 在[1,9]上就具有“DK”性质.
在[1,9]上就具有“DK”性质.
(1)判断函数f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性质?说明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
,(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)讨论函数
 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
相关试题

