【题目】如图,已知椭圆![]() :
: ![]() ,其左右焦点为
,其左右焦点为![]() 、
、![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.

(1)求椭圆![]() 的方程;
的方程;
(2)记![]() 的面积为
的面积为![]() ,
, ![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() ,试问:是否存在直线
,试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
参考答案:
【答案】(1)椭圆![]() 的方程为
的方程为![]() ;(2)方程为
;(2)方程为![]() .
.
【解析】试题分析:(1)第一问比较简单直接列一个方程组,解出a,b,c即可. (2)第二问首先需要设出直线的方程![]() (
(![]() ),再利用
),再利用![]() 和相似得到
和相似得到![]() ,化简这个方程需要点G和点D的坐标,利用韦达定理求出点G和点D的坐标代入
,化简这个方程需要点G和点D的坐标,利用韦达定理求出点G和点D的坐标代入![]() 解关于k的方程即可.
解关于k的方程即可.
试题解析:(1)因为![]() 、
、![]() 、
、![]() 构成等差数列,
构成等差数列,
所以![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)假设存在直线![]() ,使得
,使得![]() ,显然直线
,显然直线![]() 不能与
不能与![]() ,
, ![]() 轴垂直.
轴垂直.
设![]() 方程为
方程为![]() (
(![]() ),
),
将其代入![]() ,整理得
,整理得![]() ,
,
设![]() ,
, ![]() ,所以
,所以![]() ,
,
故点![]() 的横坐标为
的横坐标为![]() ,所以
,所以 ,
,
设![]() ,因为
,因为![]() ,所以
,所以 ,
,
解得![]() ,即
,即 .
.
∵![]() 和
和![]() 相似,且
相似,且![]() ,则
,则![]() ,,
,,
∴ ,
,
整理得![]() ,因此
,因此![]() ,
, ![]() ,
,
所以存在直线![]() ,方程为
,方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2,在三棱锥A-BCD中,AB=CD=4, AC=BC=AD=BD=3.
(I)证明:AB
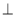 CD;
CD;(II) E在线段BC上,BE=2EC, F是线段AC的中点,求平面ADE与平面BFD所成锐二面角的余弦值
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,F(-1, 0)是椭圆
 的左焦点,过点F且方向向量为
的左焦点,过点F且方向向量为 的光线,经直线
的光线,经直线 反射后通过左顶点D
反射后通过左顶点D .
.(I)求椭圆
 的方程;
的方程;(II)过点F作斜率为
 的直线
的直线 交椭圆
交椭圆 于A, B两点,M为AB的中点,直线OM (0为原点)与直线
于A, B两点,M为AB的中点,直线OM (0为原点)与直线 交于点P,若满足
交于点P,若满足 ,求
,求 的值.
的值. -
科目: 来源: 题型:
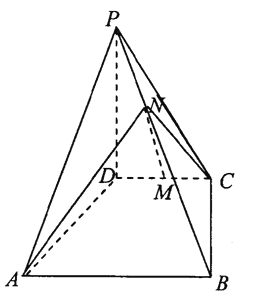
查看答案和解析>>【题目】如图四棱锥
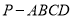 中,
中, 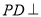 平面
平面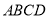 ,底面
,底面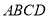 是梯形,
是梯形, 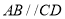 ,
, 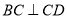 ,
, 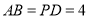 ,
, 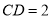 ,
, 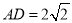 ,
, 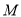 为
为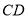 的中点,
的中点, 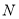 为
为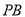 上一点,且
上一点,且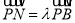 (
(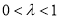 ).
).
(1)若
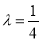 时,求证:
时,求证: 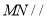 平面
平面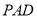 ;
;(2)若直线
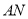 与平面
与平面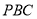 所成角的正弦值为
所成角的正弦值为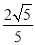 ,求异面直线
,求异面直线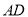 与直线
与直线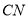 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
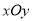 中,曲线
中,曲线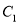 的参数方程为
的参数方程为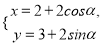 (
(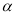 为参数,
为参数, 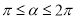 ),以原点
),以原点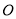 为极点,
为极点, 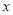 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线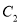 的极坐标方程为
的极坐标方程为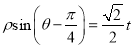 .
.(1)求曲线
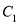 与
与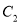 的直角坐标方程;
的直角坐标方程;(2)当
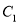 与
与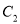 有两个公共点时,求实数
有两个公共点时,求实数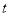 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱锥
 中,底面
中,底面 为菱形,
为菱形,  ,
,  ,
,  为棱
为棱 的中点,且
的中点,且 .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)当直线
 与底面
与底面 成
成 角时,求二面角
角时,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了适当疏导电价矛盾,保障电力供应,支持可再生能源发展,促进节能减排,安徽省于2012年推出了省内居民阶梯电价的计算标准:以一个年度为计费周期、月度滚动使用,第一阶梯电量:年用电量2160度以下(含2160度),执行第一档电价0.5653元/度;第二阶梯电量:年用电量2161至4200度(含4200度),执行第二档电价0.6153元/度;第三阶梯电量:年用电量4200度以上,执行第三档电价0.8653元/度.
某市的电力部门从本市的用电户中随机抽取10户,统计其同一年度的用电情况,列表如下表:
用户编号
1
2
3
4
5
6
7
8
9
10
年用电量(度)
1000
1260
1400
1824
2180
2423
2815
3325
4411
4600
(Ⅰ)试计算表中编号为10的用电户本年度应交电费多少元?
(Ⅱ)现要在这10户家庭中任意选取4户,对其用电情况作进一步分析,求取到第二阶梯电量的户数的分布列与期望;
(Ⅲ)以表中抽到的10户作为样本估计全市的居民用电情况,现从全市居民用电户中随机地抽取10户,若抽到
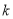 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求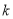 的值.
的值.
相关试题

