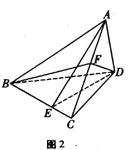
【题目】如图2,在三棱锥A-BCD中,AB=CD=4, AC=BC=AD=BD=3.
(I)证明:AB![]() CD;
CD;
(II) E在线段BC上,BE=2EC, F是线段AC的中点,求平面ADE与平面BFD所成锐二面角的余弦值
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,易证
,易证![]() ,
, ![]() ,进而得
,进而得![]() ,从而得证;
,从而得证;
(Ⅱ)过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
, ![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() ,所以AP⊥平面BDC,以
,所以AP⊥平面BDC,以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,过
轴,过![]() 作
作![]() 的平行线为
的平行线为![]() 轴,建立空间直角坐标系,分别求得面
轴,建立空间直角坐标系,分别求得面![]() 和面
和面![]() 的法向量,进而利用向量求解即可.
的法向量,进而利用向量求解即可.
试题解析:
(Ⅰ)
证明:如图2,取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
(Ⅱ)解:过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
, ![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() ,所以AP⊥平面BDC,以
,所以AP⊥平面BDC,以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,过
轴,过![]() 作
作![]() 的平行线为
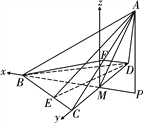
的平行线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
 ,
, ![]() ,
, ![]() ,
, ![]() ,
, 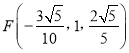 ,
, 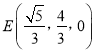 ,
, 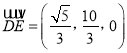 ,
, 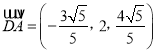 ,
, ![]() ,
, 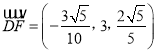 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() 解得
解得![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() 解得
解得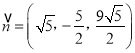 ,
,
设平面ADE与平面BFD所成的二面角为![]() ,
,
则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=x+b与函数f(x)=ln x的图象交于两个不同的点A,B,其横坐标分别为x1,x2,且x1<x2.
(1)求b的取值范围;
(2)当x2≥2时,证明x1·
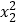 <2.
<2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex-x2+a,x∈R的图象在x=0处的切线方程为y=bx.(e≈2.718 28)
(1)求函数f(x)的解析式;
(2)当x∈R时,求证:f(x)≥-x2+x;
(3)若f(x)>kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f'(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b2>3a;
(3)若f(x),f'(x)这两个函数的所有极值之和不小于-
 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,F(-1, 0)是椭圆
 的左焦点,过点F且方向向量为
的左焦点,过点F且方向向量为 的光线,经直线
的光线,经直线 反射后通过左顶点D
反射后通过左顶点D .
.(I)求椭圆
 的方程;
的方程;(II)过点F作斜率为
 的直线
的直线 交椭圆
交椭圆 于A, B两点,M为AB的中点,直线OM (0为原点)与直线
于A, B两点,M为AB的中点,直线OM (0为原点)与直线 交于点P,若满足
交于点P,若满足 ,求
,求 的值.
的值. -
科目: 来源: 题型:
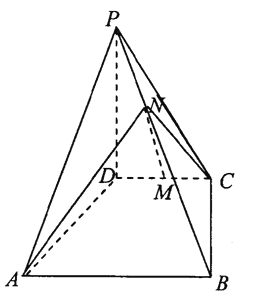
查看答案和解析>>【题目】如图四棱锥
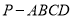 中,
中, 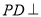 平面
平面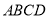 ,底面
,底面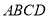 是梯形,
是梯形, 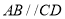 ,
, 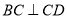 ,
, 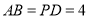 ,
, 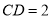 ,
, 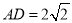 ,
, 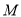 为
为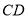 的中点,
的中点, 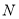 为
为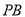 上一点,且
上一点,且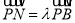 (
(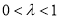 ).
).
(1)若
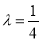 时,求证:
时,求证: 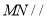 平面
平面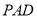 ;
;(2)若直线
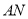 与平面
与平面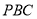 所成角的正弦值为
所成角的正弦值为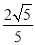 ,求异面直线
,求异面直线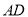 与直线
与直线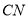 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
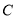 :
:  ,其左右焦点为
,其左右焦点为 、
、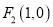 ,过点
,过点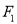 的直线交椭圆
的直线交椭圆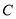 于
于 ,
,  两点,线段
两点,线段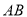 的中点为
的中点为 ,
,  的中垂线与
的中垂线与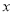 轴和
轴和 轴分别交于
轴分别交于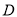 、
、 两点,且
两点,且 、
、 、
、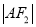 构成等差数列.
构成等差数列.
(1)求椭圆
 的方程;
的方程;(2)记
 的面积为
的面积为 ,
,  (
( 为原点)的面积为
为原点)的面积为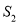 ,试问:是否存在直线
,试问:是否存在直线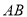 ,使得
,使得 ?说明理由.
?说明理由.
相关试题

