【题目】选修4-4,坐标系与参数方程
已知在平面直角坐标系xOy中,椭圆C的方程为![]() ,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线
,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设M(x,y)为椭圆C上任意一点,求|![]() x+y﹣1|的最大值.
x+y﹣1|的最大值.
参考答案:
【答案】(1)![]() (2)9
(2)9
【解析】试题分析:(1)根据![]() 将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|
将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|![]() x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
试题解析:(1)根据题意,椭圆C的方程为![]() +
+![]() =1,
=1,
则其参数方程为![]() ,(α为参数);
,(α为参数);
直线l的极坐标方程为ρsin(θ+![]() )=3,变形可得ρsinθcos
)=3,变形可得ρsinθcos![]() +ρcosθsin
+ρcosθsin![]() =3,
=3,
即![]() ρsinθ+
ρsinθ+![]() ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得
ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得![]() x+y﹣6=0,
x+y﹣6=0,
即直线l的普通方程为![]() x+y﹣6=0;
x+y﹣6=0;
(2)根据题意,M(x,y)为椭圆一点,则设M(2cosθ,4sinθ),
|2![]() x+y﹣1|=|4
x+y﹣1|=|4![]() cosθ+4sinθ﹣1|=|8sin(θ+
cosθ+4sinθ﹣1|=|8sin(θ+![]() )﹣1|,
)﹣1|,
分析可得,当sin(θ+![]() )=﹣1时,|2
)=﹣1时,|2![]() x+y﹣1|取得最大值9.
x+y﹣1|取得最大值9.
-
科目: 来源: 题型:
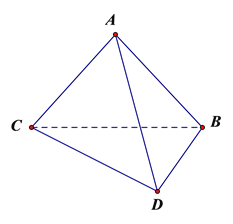
查看答案和解析>>【题目】如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,
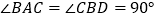 ,
,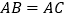 ,
,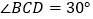 ,BC=6.
,BC=6.(1)证明:平面ADC平面ADB;
(2)求二面角A—CD—B平面角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
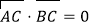 ,|BC|=2|AC|.
,|BC|=2|AC|.(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得
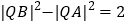 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.(3)过椭圆E上异于其顶点的任一点P,作
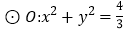 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: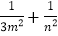 为定值.
为定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
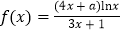 ,曲线
,曲线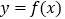 在点
在点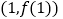 处的切线与直线
处的切线与直线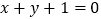 垂直.
垂直.(1)求
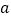 的值;
的值;(2)若对于任意的
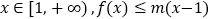 恒成立,求
恒成立,求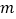 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲设函数

(1)当
 时,解不等式:
时,解不等式: ;
;(2)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 的定义域为
的定义域为 ,若满足条件:存在
,若满足条件:存在 ,使
,使 在
在 上的值域为
上的值域为 ,则称
,则称 为“倍缩函数”.若函数
为“倍缩函数”.若函数 为“倍缩函数”,则实数
为“倍缩函数”,则实数 的取值范围是
的取值范围是A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
 的各项为正数,且
的各项为正数,且 .
.(1)求
 的通项公式;
的通项公式;(2)设
 ,求证数列
,求证数列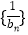 的前
的前 项和
项和 <2.
<2.
相关试题

