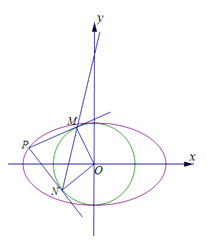
【题目】如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且![]() ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得![]() ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作![]() 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:![]() 为定值.
为定值.![]()

参考答案:
【答案】(1)![]() (2)满足条件的点Q存在,且有两个(3)见解析,
(2)满足条件的点Q存在,且有两个(3)见解析,![]()
【解析】试题分析:(1)依题意有![]() ,再根据几何条件得三角形AOC为等腰直角三角形,即得点C的坐标,代入椭圆方程可得
,再根据几何条件得三角形AOC为等腰直角三角形,即得点C的坐标,代入椭圆方程可得![]() ,(2)先用坐标化简
,(2)先用坐标化简![]() ,得点Q在直线
,得点Q在直线![]() 上,再根据直线与椭圆位置关系确定交点个数,即得满足条件的点Q个数,(3)设点
上,再根据直线与椭圆位置关系确定交点个数,即得满足条件的点Q个数,(3)设点![]() ,先利用两圆公共弦求切点弦MN方程,解得截距,根据点P在椭圆上化简
,先利用两圆公共弦求切点弦MN方程,解得截距,根据点P在椭圆上化简![]() ,得定值.
,得定值.
试题解析:(1)依题意知:椭圆的长半轴长![]() ,则A(2,0),
,则A(2,0),
设椭圆E的方程为![]()
由椭圆的对称性知|OC|=|OB| 又∵![]() ,|BC|=2|AC|
,|BC|=2|AC|
∴AC⊥BC,|OC|=|AC| ∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1) ,
将C的坐标(1,1)代入椭圆方程得![]()
∴所求的椭圆E的方程为![]()
(2)设在椭圆E上存在点Q,使得![]() ,设
,设![]() ,则
,则![]()
即点Q在直线![]() 上,
上,
∴点Q即直线![]() 与椭圆E的交点,
与椭圆E的交点,
∵直线![]() 过点
过点![]() ,而点椭圆
,而点椭圆![]() 在椭圆E的内部,
在椭圆E的内部,
∴满足条件的点Q存在,且有两个.
(3)设点![]() ,由M、N是
,由M、N是![]() 的切点知,
的切点知,![]() ,
,
∴O、M、P、N四点在同一圆上,
且圆的直径为OP,则圆心为![]() ,
,
其方程为![]() ,
,
即![]() -----④
-----④
即点M、N满足方程④,又点M、N都在![]() 上,
上,
∴M、N坐标也满足方程![]() ---------------⑤
---------------⑤
⑤-④得直线MN的方程为![]() ,
,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
∴![]() ,又点P在椭圆E上,
,又点P在椭圆E上,
∴![]() ,即
,即![]() =定值.
=定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在数列
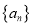 中,
中, 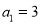 ,
, 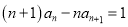 ,
, 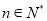 .
.(1)证明数列
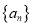 是等差数列,并求
是等差数列,并求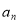 的通项公式;
的通项公式;(2)设数列
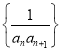 的前
的前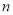 项和为
项和为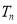 ,证明:
,证明: 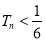 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为
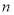 )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).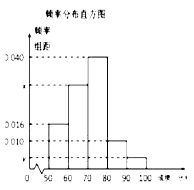

(1)求样本容量
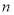 和频率分布直方图中的
和频率分布直方图中的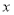 ,
,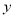 的值;
的值; (2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设
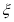 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求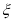 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
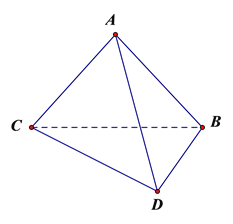
查看答案和解析>>【题目】如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,
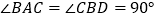 ,
,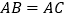 ,
,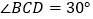 ,BC=6.
,BC=6.(1)证明:平面ADC平面ADB;
(2)求二面角A—CD—B平面角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
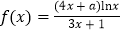 ,曲线
,曲线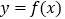 在点
在点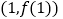 处的切线与直线
处的切线与直线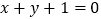 垂直.
垂直.(1)求
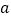 的值;
的值;(2)若对于任意的
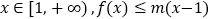 恒成立,求
恒成立,求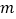 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4,坐标系与参数方程
已知在平面直角坐标系xOy中,椭圆C的方程为
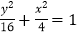 ,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线
,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线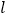 的极坐标方程为
的极坐标方程为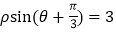 .
.(1)求直线
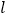 的直角坐标方程;
的直角坐标方程;(2)设M(x,y)为椭圆C上任意一点,求|
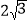 x+y﹣1|的最大值.
x+y﹣1|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲设函数

(1)当
 时,解不等式:
时,解不等式: ;
;(2)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足
 ,求证:
,求证: .
.
相关试题

