搜索
【题目】已知等比数列
的各项为正数，且
.
（1）求的通项公式；
（2）设
，求证数列
的前
项和
＜2．
参考答案：
【答案】（1）
（2）见解析
【解析】试题分析：（1）先根据条件列关于首项与公比的方程组，解出首项与公比，再代入等比数列通项公式即可，（2）先根据对数性质化简得
，再根据裂项相消法求数列
的前
项和
，最后根据n取值范围证不等式.
试题解析：（1）设数列N的公比为q，
∵9a32=a2a6，即9a22q2=a2a2q4，解得q2=9．
又q＞0，则q=3，
∵a3=2a2+9，即9a1=6a1+9，解得a1=3，
∴
．
（2）a1a2…an=31+2+3+…+n=3
，
∴bn=log3a1+log3a2+…+log3an=log3（a1a2…an）=
，
∴
．
∴
<2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】选修4-4，坐标系与参数方程
已知在平面直角坐标系xOy中，椭圆C的方程为
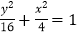，以O为极点，x轴的非负半轴为极轴，取相同的长度单位建立极坐标系，直线
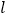的极坐标方程为
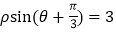．（1）求直线
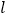的直角坐标方程；（2）设M（x，y）为椭圆C上任意一点，求|
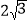x+y﹣1|的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】选修4-5：不等式选讲设函数
（1）当
时，解不等式：
；（2）若关于x的不等式f（x）≤4的解集为[﹣1，7]，且两正数s和t满足
，求证：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
的定义域为
，若满足条件：存在
，使在
上的值域为
，则称为“倍缩函数”．若函数
为“倍缩函数”，则实数
的取值范围是A. （﹣∞，ln2﹣1） B. （﹣∞，ln2﹣1]
C. （1﹣ln2，+∞） D. [1﹣ln2，+∞）
-
科目： 来源： 题型：
查看答案和解析>>【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查，其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下：
地铁站
世界之窗
白石州
高新园
深大
桃园
大新
满意度得分
70
76
72
70
72
x
已知6个站的平均得分为75分.
（1）求大新站的满意度得分x，及这6个站满意度得分的标准差；
（2）从表中前5个站中，随机地选2个站，求恰有1个站得分在区间（68，75）中的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知A、B、C是长轴长为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且
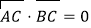，|BC|＝2|AC|．（1）求椭圆E的方程；
（2）在椭圆E上是否存点Q，使得
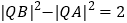？若存在，有几个（不必求出Q点的坐标），若不存在，请说明理由．（3）过椭圆E上异于其顶点的任一点P，作
的两条切线，切点分别为M、N，若直线MN在x轴、y轴上的截距分别为m、n，证明：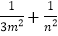
为定值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设
，曲线
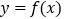在点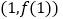
处的切线与直线
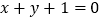垂直．（1）求
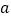的值；（2）若对于任意的
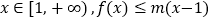恒成立，求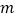
的取值范围．
相关试题
