【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 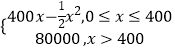 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
参考答案:
【答案】
(1)解:由于月产量为x台,则总成本为20000+100x,
从而利润f(x)= 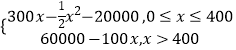
(2)解:当0≤x≤400时,f(x)=300x﹣ ![]() ﹣20000=﹣
﹣20000=﹣ ![]() (x﹣300)2+25000,
(x﹣300)2+25000,
∴当x=300时,有最大值25000;
当x>400时,f(x)=60000﹣100x是减函数,
∴f(x)=60000﹣100×400<25000.
∴当x=300时,有最大值25000,
即当月产量为300台时,公司所获利润最大,最大利润是25000元
【解析】(1)根据利润=收益﹣成本,由已知分两段当0≤x≤400时,和当x>400时,求出利润函数的解析式;(2)根据分段函数的表达式,分别求出函数的最大值即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1﹣x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为﹣4,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
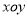 中,以坐标原点为极点,
中,以坐标原点为极点, 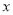 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆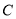 的极坐标方程为
的极坐标方程为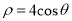 .
.(1)求出圆
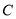 的直角坐标方程;
的直角坐标方程;(2)已知圆
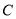 与
与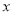 轴相交于
轴相交于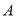 ,
, 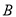 两点,直线
两点,直线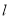 :
: 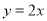 关于点
关于点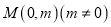 对称的直线为
对称的直线为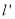 .若直线
.若直线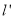 上存在点
上存在点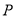 使得
使得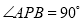 ,求实数
,求实数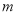 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
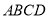 中,
中, 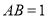 ,
, 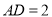 ,点
,点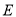 为
为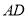 中点,沿
中点,沿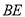 将
将 折起至
折起至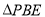 ,如下图所示,点
,如下图所示,点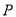 在面
在面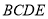 的射影
的射影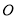 落在
落在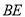 上.
上.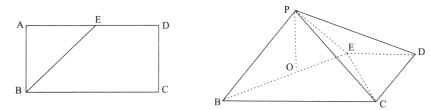
(Ⅰ)求证:
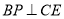 ;
;(Ⅱ)求二面角
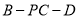 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划面向高一年级
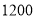 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了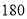 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有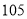 人.在这
人.在这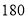 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为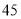 人.
人.(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的
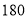 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过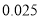 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?选择自然科学类
选择社会科学类
合计
男生
女生
合计
附:
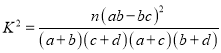 ,其中
,其中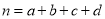 .
.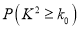
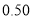

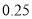
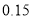
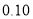
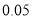
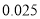

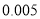
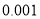


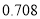
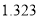
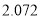
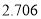
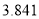
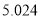
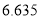
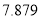
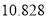
-
科目: 来源: 题型:
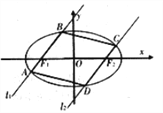
查看答案和解析>>【题目】如图,过椭圆
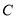 :
: 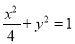 的左右焦点
的左右焦点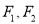 分别作直线
分别作直线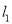 ,
, 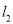 交椭圆于
交椭圆于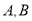 与
与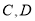 ,且
,且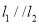 .
.
(1)求证:当直线
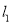 的斜率
的斜率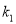 与直线
与直线 的斜率
的斜率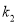 都存在时,
都存在时, 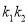 为定值;
为定值;(2)求四边形
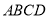 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|(a﹣1)x2﹣x+2=0}有且只有一个元素,则a= .
相关试题

