【题目】已知a>0且a≠1,函数f(x)= ![]() (a﹣x﹣ax),g(x)=﹣ax+2.
(a﹣x﹣ax),g(x)=﹣ax+2.
(1)指出f(x)的单调性(不要求证明);
(2)若有g(2)+f(2)=3,求g(﹣2)+f(﹣2)的值;
(3)若h(x)=f(x)+g(x)﹣2,求使不等式h(x2+tx)+h(4﹣x)<0恒成立的t的取值范围.
参考答案:
【答案】
(1)解:由题意:函数f(x)= ![]() (a﹣x﹣ax),
(a﹣x﹣ax),
①当0<a<1时, ![]() 递减,
递减,
②当a>1时, ![]() 递减,
递减,
∴当且a>0且a≠1时,f(x)是减函数
(2)解:由题意g(x)=﹣ax+2.
设h(x)=f(x)+g(x)﹣2,则:h(x)= ![]() ,其定义域为R,关于原点对称,
,其定义域为R,关于原点对称,
h(﹣x)= ![]() =
= ![]() =﹣[
=﹣[ ![]() ]=﹣h(x)
]=﹣h(x)
∵h(﹣x)=﹣h(x),
∴h(x)是定义域为R的奇函数.
∵g(2)+f(2)=3,则:h(2)=1,
∴h(﹣2)=﹣1,即:g(2)+f(2)﹣2=﹣1
所以g(2)+f(2)=1
(3)解:由(2)知h(x)是定义域为R的奇函数,且在R上为减函数,
由h(x2+tx)+h(4﹣x)<0,则有:h(x2+tx)<h(﹣4+x)
∴x2+tx>x﹣4,即x2+(t﹣1)x+4>0 恒成立,
∴△=b2﹣4ac=(t﹣1)2﹣16<0
解得:﹣3<t<5,
故得t的取值范围是(﹣3,5)
【解析】(1)利用指数函数的单调性,对底数a讨论,即可单调性.(2)令f(x)+g(x)﹣2=h(x).证明其奇偶性,利用奇偶性求值.(3)利用(1)(2)中的结论,将不等式转化为二次函数恒成立问题,即可求解t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
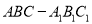 中,侧面
中,侧面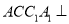 底面
底面 ,
, 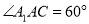 ,
, 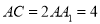 ,点
,点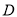 ,
, 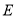 分别是
分别是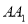 ,
, 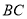 的中点.
的中点.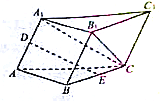
(1)证明:
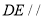 平面
平面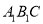 ;
;(2)若
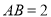 ,
, 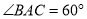 ,求直线
,求直线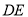 与平面
与平面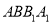 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为( )

A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
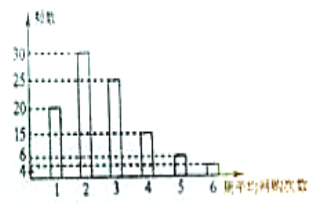
(1)根据已知条件完成下面的
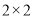 列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?网购迷
非网购迷
合计
年龄不超过40岁
年龄超过40岁
合计
(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数
 的分布列与期望.
的分布列与期望.附:
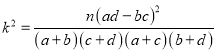 ;
;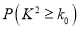
0.15
0.10
0.05
0.01
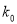
2.072
2.706
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二面角α﹣L﹣β的大小为
 ,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
A.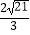
B.2
C.2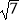
D.2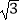
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集为R,集合A={x||x|≤2},B={x|
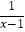 >0},则A∩RB=( )
>0},则A∩RB=( )
A.[﹣2,1)
B.[﹣2,1]
C.[﹣2,2]
D.[﹣2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )

A.
B.
C.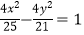
D.
相关试题

