【题目】从某学校高三年级共![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成八组,第一组
之间,将测量结果按如下方式分成八组,第一组![]() ;第二组
;第二组![]() ,
,![]() ,第八组
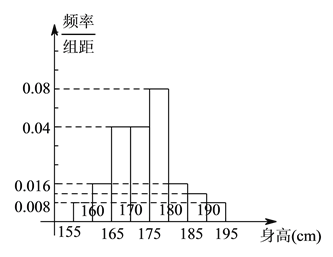
,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.

(![]() )估计这所学校高三年级全体男生身高
)估计这所学校高三年级全体男生身高![]() 以上(含
以上(含![]() )的人数.
)的人数.
(![]() )求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).
)求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).
(![]() )若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为
)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为![]() 、
、![]() ,求满足
,求满足![]() 的事件概率.
的事件概率.
参考答案:
【答案】(1)9人;(2)见解析;(3)![]()
【解析】试题分析:(1)由频率分布直方图可得前五组频率,进而可得后三组频率和人数,又可得后三组的人数,可得平均身高;
(2)易得后三组的![]() ,可得频率分布直方图;
,可得频率分布直方图;
(3)由(![]() )知身高在
)知身高在![]() 内的人数为
内的人数为![]() 人,
人,
设![]() ,
,![]() ,
,![]() ,
,![]() 。身高为
。身高为![]() 的人数为
的人数为![]() 人,
人,
设为![]() ,
,![]() .,列举可得总的基本事件共15种情况,事件“
.,列举可得总的基本事件共15种情况,事件“![]() ”所包含的基本事件个数有6+1=7,由概率公式可得.
”所包含的基本事件个数有6+1=7,由概率公式可得.
试题解析:(![]() )由频率分布直方图知,
)由频率分布直方图知,
前五组频率为![]() ,
,
后三组频率为![]() ,人数为
,人数为![]() 人,
人,
这所学校高三男生身高在![]() 以上(含
以上(含![]() )的人数为
)的人数为![]() 人.
人.
(![]() )由频率分布直方图得第八组频率为
)由频率分布直方图得第八组频率为![]() ,人数为
,人数为![]() 人,
人,
设第六组人数为![]() ,则第七组人数为
,则第七组人数为![]() ,又
,又![]() ,所以
,所以![]() ,
,
即第六组人数为![]() 人,第七组人数为
人,第七组人数为![]() 人,频率分别为
人,频率分别为![]() ,
,![]() ,
,
频率除以组距分别等于![]() ,
,![]() ,见图.
,见图.
(![]() )由(
)由(![]() )知身高在
)知身高在![]() 内的人数为
内的人数为![]() 人,
人,
设![]() ,
,![]() ,
,![]() ,
,![]() 。身高为
。身高为![]() 的人数为
的人数为![]() 人,
人,
设为![]() ,
,![]() .
.
若![]() ,
,![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共六种情况.
共六种情况.
若![]() ,
,![]() 时,有
时,有![]() 共一种情况.
共一种情况.
若![]() ,
,![]() 分别在
分别在![]() ,
,![]() 内时,
内时,
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共
共![]() 种情况.
种情况.
所以基本事件的总数为![]() 种.
种.
事件![]() 所包含的基本事件个数有
所包含的基本事件个数有![]() 种,故
种,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.(1)证明:
 ;
;(2)是否存在一点
 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,前n项和为Sn , 且Sn=
 ,数列{bn}的前n项和为Tn , 且bn=
,数列{bn}的前n项和为Tn , 且bn= 
(1)求数列{an}的通项公式;
(2)是否存在m,n∈N* , 使得Tn=am , 若存在,求出所有满足题意的m,n,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一动圆与圆
 外切,与圆
外切,与圆 内切.
内切.(1)求动圆圆心
 的轨迹
的轨迹 的方程.
的方程.(2)设过圆心
 的直线
的直线 与轨迹
与轨迹 相交于
相交于 两点,
两点, (
( 为圆
为圆 的圆心)的内切圆
的圆心)的内切圆 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
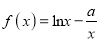 ,a为常数
,a为常数(1)判断f(x)在定义域内的单调性
(2)若f(x)在
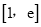 上的最小值为
上的最小值为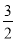 ,求a的值
,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,经过点
中,经过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 和
和 .
.(1)求
 的取值范围;
的取值范围;(2)设椭圆与
 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知矩形
 的长为2,宽为1,
的长为2,宽为1, .
. 边分别在
边分别在 轴.
轴. 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图所示)。将矩形折叠,使
点与坐标原点重合(如图所示)。将矩形折叠,使 点落在线段
点落在线段 上。
上。
(1)若折痕所在直线的斜率为
 ,试求折痕所在直线的方程;
,试求折痕所在直线的方程;(2)当
 时,求折痕长的最大值;
时,求折痕长的最大值; (3)当
 时,折痕为线段
时,折痕为线段 ,设
,设 ,试求
,试求 的最大值。
的最大值。
相关试题

