【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若![]() ,试讨论关于
,试讨论关于![]() 的方程
的方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
参考答案:
【答案】(1)当![]() 时,函数
时,函数![]() 无极值,当
无极值,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,无极大值;
,无极大值;
(2)方程![]() 有唯一解.
有唯一解.
【解析】
试题分析:(1)求出函数![]() 定义域,求导,令
定义域,求导,令![]() .利用导函数的符号,判断函数的单调性,求
.利用导函数的符号,判断函数的单调性,求
出函数的极值;(2)令![]() ,对其求导,分为
,对其求导,分为![]() 和
和![]() 两种情形,根据导数与
两种情形,根据导数与![]() 的关系,判断函数的单调性,根据其大致图象得到其与
的关系,判断函数的单调性,根据其大致图象得到其与![]() 轴的交点分数,故而得到方程解的个数.
轴的交点分数,故而得到方程解的个数.
试题解析:(1)依题意得,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 无极值;
无极值;
当![]() 时,
时,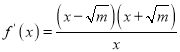 ,
,
令![]() ,得
,得![]() ,函数
,函数![]() 单调递减,
单调递减,
令![]() ,得
,得![]() ,函数
,函数![]() 单调递增,
单调递增,
故函数![]() 有极小值
有极小值![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(2)令![]() ,
,![]() ,问题等价于求
,问题等价于求![]() 函数的零点个数.
函数的零点个数.
易得![]() .
.
①若![]() ,则
,则![]() ,函数
,函数![]() 为减函数,
为减函数,
注意到![]() ,
,![]() ,所以
,所以![]() 有唯一零点;
有唯一零点;
②若![]() ,则当
,则当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
注意到![]() ,
,![]() ,所以
,所以![]() 有唯一零点.
有唯一零点.
综上,若![]() ,函数
,函数![]() 有唯一零点,即方程
有唯一零点,即方程![]() 有唯一解.
有唯一解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男
女
总计
喜欢
40
20
60
不喜欢
20
30
50
总计
60
50
110
由
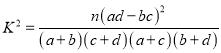 算得
算得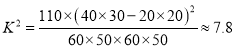 .
.附表:
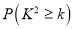
0.050
0.010
0.001
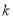
3.841
6.635
10.828
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过
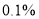 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”B. 在犯错误的概率不超过
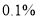 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”C. 有
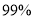 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”D. 有
以上的把握认为“喜欢该节目与性别无关” -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
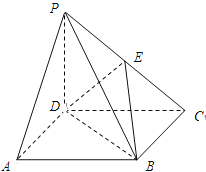
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角EBDP的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次水下考古活动中,某一潜水员需潜水
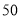 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为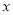 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为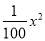 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少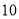 分钟最多
分钟最多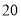 分钟,每分钟用氧量为
分钟,每分钟用氧量为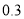 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为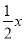 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为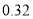 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为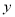 升.
升.(1)如果水底作业时间是
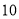 分钟,将
分钟,将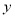 表示为
表示为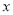 的函数;
的函数;(2)若
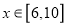 ,水底作业时间为
,水底作业时间为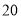 分钟,求总用氧量
分钟,求总用氧量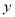 的取值范围;
的取值范围;(3)若潜水员携带氧气
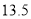 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是 ( )
A. 如果平面
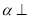 平面
平面 ,那么平面
,那么平面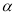 内一定存在直线平行于平面
内一定存在直线平行于平面
B. 如果平面
 不垂直平面
不垂直平面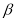 ,那么平面
,那么平面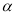 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面
C. 如果平面
 平面
平面 ,平面
,平面 平面
平面 ,且
,且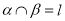 ,那么
,那么
D. 如果平面
 平面
平面 ,那么平面
,那么平面 内所有直线都垂直于平面
内所有直线都垂直于平面
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级某次数学竞赛随机抽取
 名学生的成绩,分组为
名学生的成绩,分组为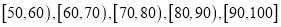 ,统计后得到频率分布直方图如图所示:
,统计后得到频率分布直方图如图所示: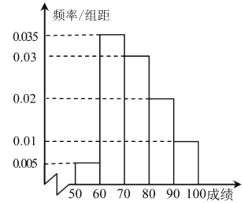
(1)试估计这组样本数据的众数和中位数(结果精确到
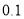 );
);(2)年级决定在成绩
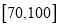 中用分层抽样抽取
中用分层抽样抽取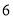 人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在
人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在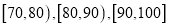 这三组分別抽取了多少人?
这三组分別抽取了多少人?(3)现在要从(2)中抽取的
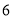 人中选出正副
人中选出正副 个小组长,求成绩在
个小组长,求成绩在 中至少有
中至少有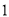 人当选为正、副小组长的概率.
人当选为正、副小组长的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
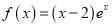 .
.(1)求
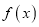 在
在 上的最小值
上的最小值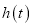 ;
;(2)若存在两个不同的实数
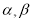 ,使得
,使得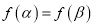 ,求证:
,求证: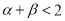 .
.
相关试题

