【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
参考答案:
【答案】D
【解析】由题意可知: ![]() 、结合实物:教室的门面与地面垂直,门面的上棱对应的直线就与地面平行,故此命题成立;
、结合实物:教室的门面与地面垂直,门面的上棱对应的直线就与地面平行,故此命题成立; ![]() 、假若平面
、假若平面![]() 内存在直线垂直于平面
内存在直线垂直于平面![]() ,根据面面垂直的判定定理可知两平面垂直,故此命题成立;
,根据面面垂直的判定定理可知两平面垂直,故此命题成立; ![]() 、结合面面垂直的性质可以分别在
、结合面面垂直的性质可以分别在![]() 、
、![]() 内作异于
内作异于![]() 的直线垂直于交线,再由线面垂直的性质定理可知所作的垂线平行,进而得到线面平行再由线面平行的性质可知所作的直线与
的直线垂直于交线,再由线面垂直的性质定理可知所作的垂线平行,进而得到线面平行再由线面平行的性质可知所作的直线与![]() 平行,又∵两条平行线中的一条垂直于平面那么另一条也垂直于平面,故命题成立;
平行,又∵两条平行线中的一条垂直于平面那么另一条也垂直于平面,故命题成立; ![]() 、举反例:教室内侧墙面与地面垂直,而侧墙面内有很多直线是不垂直与地面的,故此命题错误,故选
、举反例:教室内侧墙面与地面垂直,而侧墙面内有很多直线是不垂直与地面的,故此命题错误,故选![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
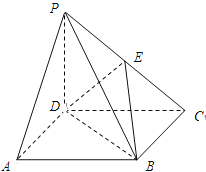
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角EBDP的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次水下考古活动中,某一潜水员需潜水
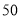 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为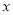 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为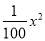 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少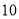 分钟最多
分钟最多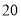 分钟,每分钟用氧量为
分钟,每分钟用氧量为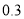 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为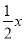 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为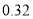 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为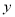 升.
升.(1)如果水底作业时间是
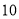 分钟,将
分钟,将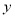 表示为
表示为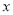 的函数;
的函数;(2)若
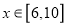 ,水底作业时间为
,水底作业时间为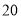 分钟,求总用氧量
分钟,求总用氧量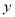 的取值范围;
的取值范围;(3)若潜水员携带氧气
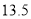 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
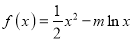 .
.(1)求函数
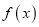 的极值;
的极值;(2)若
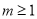 ,试讨论关于
,试讨论关于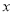 的方程
的方程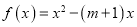 的解的个数,并说明理由.
的解的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级某次数学竞赛随机抽取
 名学生的成绩,分组为
名学生的成绩,分组为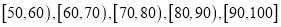 ,统计后得到频率分布直方图如图所示:
,统计后得到频率分布直方图如图所示: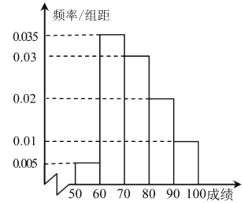
(1)试估计这组样本数据的众数和中位数(结果精确到
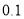 );
);(2)年级决定在成绩
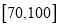 中用分层抽样抽取
中用分层抽样抽取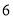 人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在
人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在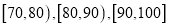 这三组分別抽取了多少人?
这三组分別抽取了多少人?(3)现在要从(2)中抽取的
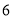 人中选出正副
人中选出正副 个小组长,求成绩在
个小组长,求成绩在 中至少有
中至少有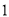 人当选为正、副小组长的概率.
人当选为正、副小组长的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
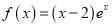 .
.(1)求
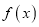 在
在 上的最小值
上的最小值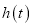 ;
;(2)若存在两个不同的实数
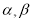 ,使得
,使得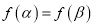 ,求证:
,求证: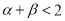 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的一种产品的广告费用
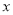 (单位:万元)与销售额
(单位:万元)与销售额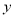 (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:广告费用
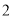
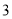
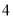
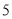
销售额
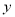
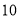
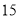

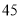
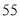
(1)根据上述数据,求出销售额
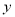 (万元)关于广告费用
(万元)关于广告费用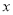 (万元)的线性回归方程;
(万元)的线性回归方程;(2)如果企业要求该产品的销售额不少于
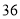 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?(参考数值:
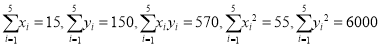 .
.回归直线的斜率和截距的最小二乘法估计公式分别为:
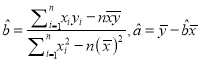 )
)
相关试题

