【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 上的最小值
上的最小值![]() ;
;
(2)若存在两个不同的实数![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)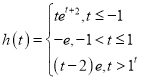 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)对![]() 进行求导,得到其单调性,在
进行求导,得到其单调性,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,对导函数的零点与所给区间
上单调递增,对导函数的零点与所给区间![]() 的关系进行讨论,即分为
的关系进行讨论,即分为![]() ,
,![]() 和
和![]() 三种情形,根据单调性求得最值;(2)令
三种情形,根据单调性求得最值;(2)令![]() ,易得当
,易得当![]() 时,
时,![]() ,设
,设![]() ,
,![]() ,故
,故![]() ,根据单调性得证.
,根据单调性得证.
试题解析:(1)根据题意,得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时
时![]() .
.
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
所以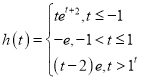 .
.
(2)构造函数![]() ,
,
则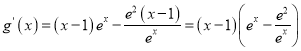 .
.
因为![]() ,所以
,所以![]() ,函数
,函数![]() 单调递增,
单调递增,
所以![]() ,
,
所以在区间![]() 上
上![]() ,所以在区间
,所以在区间![]() 上
上![]() 单调递增,
单调递增,
所以![]() ,所以当
,所以当![]() 时,
时,![]() .
.
根据(1)中![]() 的性质,若存在两个不同的实数
的性质,若存在两个不同的实数![]() ,使得
,使得![]() ,不妨设,则一定有
,不妨设,则一定有![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,
,
因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
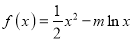 .
.(1)求函数
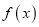 的极值;
的极值;(2)若
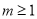 ,试讨论关于
,试讨论关于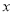 的方程
的方程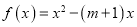 的解的个数,并说明理由.
的解的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是 ( )
A. 如果平面
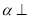 平面
平面 ,那么平面
,那么平面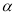 内一定存在直线平行于平面
内一定存在直线平行于平面
B. 如果平面
 不垂直平面
不垂直平面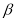 ,那么平面
,那么平面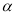 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面
C. 如果平面
 平面
平面 ,平面
,平面 平面
平面 ,且
,且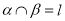 ,那么
,那么
D. 如果平面
 平面
平面 ,那么平面
,那么平面 内所有直线都垂直于平面
内所有直线都垂直于平面
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级某次数学竞赛随机抽取
 名学生的成绩,分组为
名学生的成绩,分组为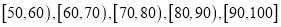 ,统计后得到频率分布直方图如图所示:
,统计后得到频率分布直方图如图所示: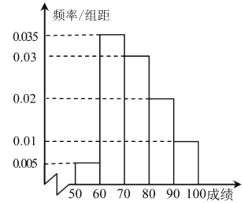
(1)试估计这组样本数据的众数和中位数(结果精确到
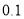 );
);(2)年级决定在成绩
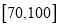 中用分层抽样抽取
中用分层抽样抽取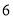 人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在
人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在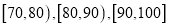 这三组分別抽取了多少人?
这三组分別抽取了多少人?(3)现在要从(2)中抽取的
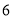 人中选出正副
人中选出正副 个小组长,求成绩在
个小组长,求成绩在 中至少有
中至少有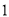 人当选为正、副小组长的概率.
人当选为正、副小组长的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的一种产品的广告费用
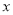 (单位:万元)与销售额
(单位:万元)与销售额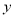 (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:广告费用
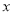
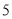
销售额
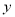
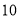
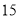

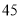
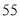
(1)根据上述数据,求出销售额
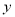 (万元)关于广告费用
(万元)关于广告费用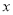 (万元)的线性回归方程;
(万元)的线性回归方程;(2)如果企业要求该产品的销售额不少于
 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?(参考数值:
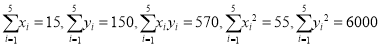 .
.回归直线的斜率和截距的最小二乘法估计公式分别为:
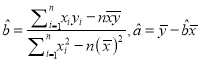 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某科研小组研究发现:一棵水蜜桃树的产量
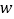 (单位:百千克)与肥料费用
(单位:百千克)与肥料费用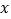 (单位:百元)满足如下关系:
(单位:百元)满足如下关系: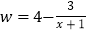 ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)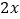 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为 (单位:百元).
(单位:百元).(1)求利润函数
 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
相关试题

