【题目】在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
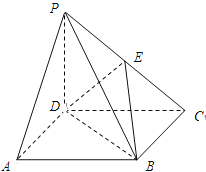
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角EBDP的余弦值.
参考答案:
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)几何法:连接![]() ,连接
,连接![]() ,根据线面平行的判定定理可先证明线线平行,即证明
,根据线面平行的判定定理可先证明线线平行,即证明![]() ;向量法:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,求平面
;向量法:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,求平面![]() 的法向量
的法向量![]() ,若
,若![]() ,说明
,说明![]() 与法向量垂直,即
与法向量垂直,即![]() 与平面平行;
与平面平行;
(Ⅱ)向量法求二面角的余弦值,即先求两个平面的法向量,而平面![]() 的法向量就是
的法向量就是![]() ,即求
,即求![]() .
.
试题解析:解:(Ⅰ)法一:以点D为原点,DA为x轴,DC为y轴,DP为z轴建立直角坐标系,设正方形的边长为1,则
![]()
∴![]() ,
,![]() .
.
设平面EBD的法向量为![]() ,
,
可求得![]() ,∴
,∴![]() ,∴
,∴![]() ∥平面EBD.
∥平面EBD.
即PA∥平面EBD.
法二:连接AC,设AC∩BD=O,连接OE,则OE∥PA,∴PA∥平面EBD.
(Ⅱ)设平面PBD的法向量为![]() .
.
∴![]() ,∴二面角E-BD-P的平面角的余弦值为
,∴二面角E-BD-P的平面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
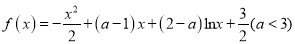 .
.(1)求曲线
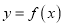 在点
在点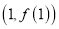 处的切线方程;
处的切线方程;(2)讨论函数
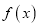 的单调区间.
的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
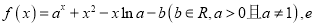 是自然对数的底数.
是自然对数的底数.(1)讨论函数
 在
在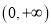 上的单调性;
上的单调性;(2)当
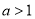 时,若存在
时,若存在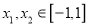 ,使得
,使得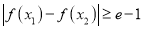 ,求实数
,求实数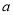 的取值范围.(参考公式:
的取值范围.(参考公式: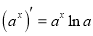 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男
女
总计
喜欢
40
20
60
不喜欢
20
30
50
总计
60
50
110
由
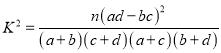 算得
算得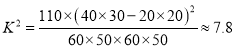 .
.附表:
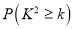
0.050
0.010
0.001
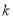
3.841
6.635
10.828
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过
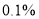 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”B. 在犯错误的概率不超过
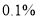 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”C. 有
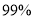 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”D. 有
以上的把握认为“喜欢该节目与性别无关” -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次水下考古活动中,某一潜水员需潜水
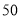 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为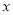 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为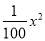 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少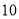 分钟最多
分钟最多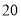 分钟,每分钟用氧量为
分钟,每分钟用氧量为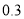 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为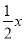 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为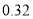 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为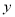 升.
升.(1)如果水底作业时间是
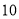 分钟,将
分钟,将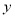 表示为
表示为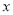 的函数;
的函数;(2)若
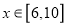 ,水底作业时间为
,水底作业时间为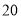 分钟,求总用氧量
分钟,求总用氧量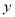 的取值范围;
的取值范围;(3)若潜水员携带氧气
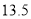 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
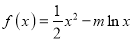 .
.(1)求函数
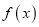 的极值;
的极值;(2)若
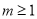 ,试讨论关于
,试讨论关于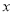 的方程
的方程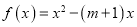 的解的个数,并说明理由.
的解的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是 ( )
A. 如果平面
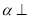 平面
平面 ,那么平面
,那么平面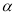 内一定存在直线平行于平面
内一定存在直线平行于平面
B. 如果平面
 不垂直平面
不垂直平面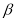 ,那么平面
,那么平面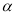 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面
C. 如果平面
 平面
平面 ,平面
,平面 平面
平面 ,且
,且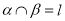 ,那么
,那么
D. 如果平面
 平面
平面 ,那么平面
,那么平面 内所有直线都垂直于平面
内所有直线都垂直于平面
相关试题

