【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其焦点与双曲线
,其焦点与双曲线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点
的右顶点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
①设![]() ,当
,当![]() 为定值时,求
为定值时,求![]() 的值;
的值;
②设点![]() 是椭圆
是椭圆![]() 上的一点,满足
上的一点,满足![]() ,记
,记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2) ①.
;(2) ①.![]() ;②.
;②. ![]() .
.
【解析】
试题分析:
(1)由题意结合几何关系可求得![]() .则椭圆的方程为
.则椭圆的方程为![]() .
.
(2)①.由题意可得双曲线![]() 右顶点为
右顶点为![]() .分类讨论:
.分类讨论:
当直线![]() 的斜率存在时,联立直线方程与椭圆方程有
的斜率存在时,联立直线方程与椭圆方程有![]() ,则
,则![]() 时
时![]() 为定值
为定值![]() .当直线
.当直线![]() 的斜率不存在时,也满足
的斜率不存在时,也满足![]() ,则当
,则当![]() 时
时![]() 为定值
为定值![]() .
.
②.当直线斜率存在时,由题意结合平行关系可得![]() .换元后利用二次函数的性质可得
.换元后利用二次函数的性质可得![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)由题意得椭圆的焦点在![]() 轴上,设方程为
轴上,设方程为![]() ,
,
其左右焦点为![]() ,所以
,所以![]() ,
,
又因为椭圆的短轴的两个端点与![]() 构成正三角形,所以
构成正三角形,所以![]()
又因为![]() ,所以
,所以![]() .
.
所以椭圆的方程为![]() .
.
(2)①双曲线![]() 右顶点为
右顶点为![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]()
由 得
得![]()
设直线![]() 与椭圆
与椭圆![]() 交点
交点![]() ,
,
则![]() ,
,
则![]() ,
,
所以![]()
![]()
![]()
![]()
![]()
当![]() ,即
,即![]() 时
时![]() 为定值
为定值![]() .
.
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]()
由 得
得![]() ,不妨设
,不妨设![]() ,由
,由![]() 可得.
可得.
![]() ,所以
,所以![]() .
.
综上所述当![]() 时
时![]() 为定值
为定值![]() .
.
②因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]()
![]()
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() .
.
令![]() ,则
,则![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]()
当直线![]() 的斜率不存在时,
的斜率不存在时,![]()
综上所述![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l过抛物线E:y2=2px(p>0)的焦点F且与x垂直,l与E所围成的封闭图形的面积为24,若点P为抛物线E上任意一点,A(4,1),则|PA|+|PF|的最小值为( )
A.6
B.4+2
C.7
D.4+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意x∈[﹣1,1],不等式﹣4≤x3+3|x﹣a|≤4恒成立,则实数a的取值范围为( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[0, ]
]
D.[0,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,已知四边形ABCD,CD⊥AD,∠CBD=
 ,AD=5,AB=7,且cos2∠ADB+3cos∠ADB=1,则BC的长为 .
,AD=5,AB=7,且cos2∠ADB+3cos∠ADB=1,则BC的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn 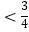 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多面体ABC﹣A1B1C1中,底面△ABC为等边三角形,边长为2,AA1⊥平面ABC,四边形A1ACC1为直角梯形,CC1与平面ABC所成的角为
 ,AA1=1
,AA1=1 
(1)若P为AB的中点,求证:A1P∥平面BC1C;
(2)求二面角A1﹣BC1﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱ABC A 1B1C1的侧棱长和底面边长均为2,D是BC 的中点.

(1) 求证:AD⊥平面B1BC C1;
(2) 求证:A 1B//平面ADC1;
(3) 求三棱锥C1 ADB1的体积.
相关试题

