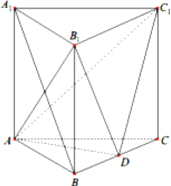
【题目】如图,正三棱柱ABC A 1B1C1的侧棱长和底面边长均为2,D是BC 的中点.

(1) 求证:AD⊥平面B1BC C1;
(2) 求证:A 1B//平面ADC1;
(3) 求三棱锥C1 ADB1的体积.
参考答案:
【答案】(1)证明略.(2)证明略.(3). ![]()
【解析】
试题分析:(1)利用线面垂直的性质,可得![]() 由正三角形的性质可得
由正三角形的性质可得![]() ,根据线面垂直的判定定理即可证明
,根据线面垂直的判定定理即可证明![]() 平面
平面![]() ;(2)连接
;(2)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,利用
,利用![]() 为
为![]() 中位线,可得
中位线,可得![]() ,利用线面的平行的判定定理,可证
,利用线面的平行的判定定理,可证![]() 平面
平面![]() ;(3)利用等体积
;(3)利用等体积![]() ,根据棱锥的体积公式可得结论.
,根据棱锥的体积公式可得结论.
试题解析:(1)证明:![]() 是正三棱柱,
是正三棱柱,![]() 平面
平面![]() ,
,![]()
平面![]() 是正三角形,
是正三角形,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() .
.
证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由
,由![]() 是正三棱柱,得四边形
是正三棱柱,得四边形![]() 为矩形,
为矩形,![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中位线,
中位线,![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(3) ![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(2)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点
的中心在坐标原点 ,其焦点与双曲线
,其焦点与双曲线 的焦点重合,且椭圆
的焦点重合,且椭圆 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.(1)求椭圆
 的方程;
的方程;(2)过双曲线
 的右顶点
的右顶点 作直线
作直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 .
.①设
 ,当
,当 为定值时,求
为定值时,求 的值;
的值;②设点
 是椭圆
是椭圆 上的一点,满足
上的一点,满足 ,记
,记 的面积为
的面积为 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn 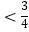 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多面体ABC﹣A1B1C1中,底面△ABC为等边三角形,边长为2,AA1⊥平面ABC,四边形A1ACC1为直角梯形,CC1与平面ABC所成的角为
 ,AA1=1
,AA1=1 
(1)若P为AB的中点,求证:A1P∥平面BC1C;
(2)求二面角A1﹣BC1﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
车型
A型
B型
C型
频数
20
40
40
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:价格(万元)
25
23.5
22
20.5
销售量(辆)
30
33
36
39
已知A型汽车的购买量y与价格x符合如下线性回归方程:
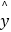 =
= 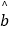 x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】己知圆
 的圆心在直线
的圆心在直线 上,且过点
上,且过点 ,与直线
,与直线 相切.
相切.(
 )求圆
)求圆 的方程.
的方程.(
 )设直线
)设直线 与圆
与圆 相交于
相交于 ,
, 两点.求实数
两点.求实数 的取值范围.
的取值范围.(
 )在(
)在( )的条件下,是否存在实数
)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,F是椭圆P:
 (a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为
(a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为 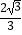 ,
,
(1)求椭圆P的方程;
(2)过点Q(﹣1,0)的直线l交椭圆P于M、N两点,交直线x=﹣4于点E, =
=  ,
,  =
=  ,证明:λ+μ为定值.
,证明:λ+μ为定值.
相关试题

