【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn ![]() .
.
参考答案:
【答案】
(1)解:∵各项为正的等比数列{an}的前n项和为Sn,S4=30,
过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1),
∴  ,
,
解得 ![]() ,q=4,
,q=4,
∴an= ![]() .
.
(2)解:∵bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴数列{bn}的前n项和:
Tn= ![]() (
( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() )
)
= ![]() (
( ![]() ﹣
﹣ ![]() )
)
= ![]() (
( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
< ![]() .
.
∴对于任意n∈N*,都有Tn ![]()
【解析】(1)利用等比数列前n项和公式及直线的方向向量性质列出方程组,由此能求出首项和公比,从而能求出数列{an}的通项公式.(2)由bn= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),利用裂项法能证明对于任意n∈N* , 都有Tn
),利用裂项法能证明对于任意n∈N* , 都有Tn ![]() .
.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意x∈[﹣1,1],不等式﹣4≤x3+3|x﹣a|≤4恒成立,则实数a的取值范围为( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[0, ]
]
D.[0,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,已知四边形ABCD,CD⊥AD,∠CBD=
 ,AD=5,AB=7,且cos2∠ADB+3cos∠ADB=1,则BC的长为 .
,AD=5,AB=7,且cos2∠ADB+3cos∠ADB=1,则BC的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点
的中心在坐标原点 ,其焦点与双曲线
,其焦点与双曲线 的焦点重合,且椭圆
的焦点重合,且椭圆 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.(1)求椭圆
 的方程;
的方程;(2)过双曲线
 的右顶点
的右顶点 作直线
作直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 .
.①设
 ,当
,当 为定值时,求
为定值时,求 的值;
的值;②设点
 是椭圆
是椭圆 上的一点,满足
上的一点,满足 ,记
,记 的面积为
的面积为 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多面体ABC﹣A1B1C1中,底面△ABC为等边三角形,边长为2,AA1⊥平面ABC,四边形A1ACC1为直角梯形,CC1与平面ABC所成的角为
 ,AA1=1
,AA1=1 
(1)若P为AB的中点,求证:A1P∥平面BC1C;
(2)求二面角A1﹣BC1﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱ABC A 1B1C1的侧棱长和底面边长均为2,D是BC 的中点.

(1) 求证:AD⊥平面B1BC C1;
(2) 求证:A 1B//平面ADC1;
(3) 求三棱锥C1 ADB1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
车型
A型
B型
C型
频数
20
40
40
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:价格(万元)
25
23.5
22
20.5
销售量(辆)
30
33
36
39
已知A型汽车的购买量y与价格x符合如下线性回归方程:
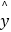 =
= 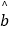 x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
相关试题

