【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 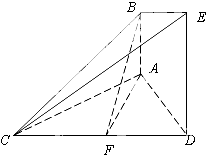
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
参考答案:
【答案】
(1)证明:取CE的中点G,连FG、BG.
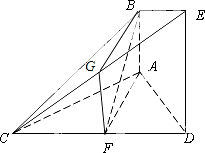
∵F为CD的中点,
∴GF∥DE且GF= ![]() DE.
DE.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.
又AB= ![]() DE,∴GF=AB.
DE,∴GF=AB.
∴四边形GFAB为平行四边形,则AF∥BG.
∵AF平面BCE,BG平面BCE,
∴AF∥平面BCE.
(2)证明:∵△ACD为等边三角形,F为CD的中点,
∴AF⊥CD.
∵DE⊥平面ACD,AF平面ACD,
∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,
∴BG⊥平面CDE.
∵BG平面BCE,
∴平面BCE⊥平面CDE
【解析】(1)取CE的中点G,连结FG、BG.由已知条件推导出四边形GFAB为平行四边形,由此能证明AF∥平面BCE.(2)由等边三角形性质得AF⊥CD,由线面垂直得DE⊥AF,从而AF⊥平面CDE,由平行线性质得BG⊥平面CDE,由此能证明平面BCE⊥平面CDE
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与圆
与圆  且与椭圆
且与椭圆 相交于
相交于 两点.
两点.
(1)若直线
 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长
(2)设直线
 的斜率分别为
的斜率分别为 ,判断
,判断 是否为定值,并说明理由
是否为定值,并说明理由(3)求
 ,面积的最小值.
,面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想将短轴长为2,长轴长为4的一个半椭圆形纸片剪成等腰梯形ABDE,且梯形ABDE内接于半椭圆,DE∥AB,AB为短轴,OC为长半轴
(1)求梯形ABDE上底边DE与高OH长的关系式;
(2)若半椭圆上到H的距离最小的点恰好为C点,求底边DE的取值范围

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,若圆C的圆心在第一象限,圆C与x轴相交于A(1,0)、B(3,0)两点,且与直线x﹣y+1=0相切,则圆C的标准方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
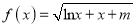 ,若曲线
,若曲线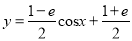 上存在
上存在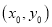 ,使得
,使得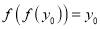 成立,则实数
成立,则实数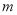 的取值范围为( )
的取值范围为( )A.
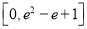 B.
B. 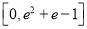 C.
C. 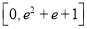 D.
D. 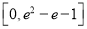
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,过点
,过点 作直线
作直线 交圆
交圆 于
于 两点,分别过
两点,分别过 两点作圆的切线,当两条切线相交于点
两点作圆的切线,当两条切线相交于点 时,则点
时,则点 的轨迹方程为__________.
的轨迹方程为__________. -
科目: 来源: 题型:
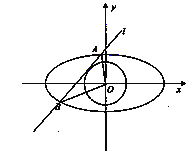
查看答案和解析>>【题目】如图,直线
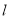 与圆O:
与圆O: 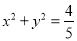 且与椭圆C:
且与椭圆C: 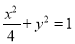 相交于A,B两点
相交于A,B两点(1)若直线
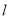 恰好经过椭圆的左顶点,求弦长AB;
恰好经过椭圆的左顶点,求弦长AB;(2)设直线OA,OB的斜率分别为k1,k2,判断k1·k2是否为定值,并说明理由
相关试题

