【题目】已知函数![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若对任意的![]() ,
,![]() ,
,![]() 恒有
恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 内单调递减;
内单调递减;![]() 时,函数
时,函数![]() 在区间
在区间![]() ,
,![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数,当
上为增函数,当![]() 时,在区间
时,在区间![]() ,
,![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数;(2)
上为增函数;(2)![]() .
.
【解析】
试题分析:(1)先对函数![]() 求导,比较
求导,比较![]() 的大小关系,得出单调区间;(2)恒成立问题的转化,求出函数
的大小关系,得出单调区间;(2)恒成立问题的转化,求出函数![]() 的最大值,得出结果.
的最大值,得出结果.
试题解析:(1)![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在定义域
在定义域![]() 内单调递减;
内单调递减;
当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() ,
,![]() 单调递减,在区间
单调递减,在区间![]() 上
上![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() ,
,![]() 单调递减,在区间
单调递减,在区间![]() 上
上![]() ,
,![]() 单调递增.
单调递增.
(2)由(1)知当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递减;
单调递减;
所以当![]() 时,
时,![]() ,
,![]() .
.
问题等价于:对任意的![]() ,恒有
,恒有![]() 成立,
成立,
即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆
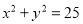 内”的概率.
内”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市有一块半径为40 m的半圆形绿化区域(以O 为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
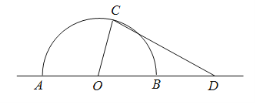
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 与
与 均为菱形,
均为菱形,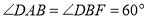 ,且
,且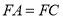 .
.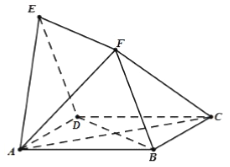
(1)求证:
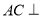 平面
平面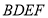 ;
;(2)求证:
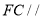 平面
平面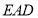 ;
;(3)求二面角
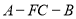 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且
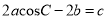 .
.(1)求角A的大小;
(2)若
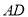 是
是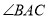 的角平分线,
的角平分线, 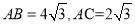 ,求
,求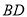 的长.
的长.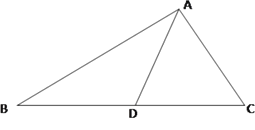
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
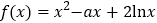 (其中
(其中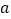 是实数)
是实数)(1)求
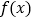 的单调区间;
的单调区间;(2)若设
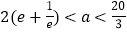 ,且
,且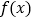 有两个极值点
有两个极值点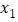 ,
,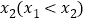 ,求
,求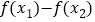 取值范围.(其中
取值范围.(其中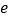 为自然对数的底数)
为自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
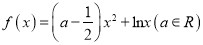 .
.(1)当
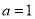 时,求
时,求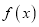 在区间
在区间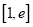 上的最大值和最小值;
上的最大值和最小值;(2)若在区间
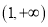 上,函数
上,函数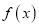 的图像恒在直线
的图像恒在直线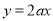 下方,求
下方,求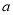 的取值范围.
的取值范围.
相关试题

