【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
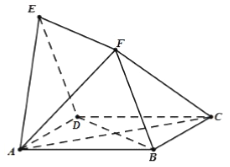
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由线面垂直的判定定理得到结论;(2)通过证明线线平行,得到线面平行;(3)建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量,易知
的法向量,易知![]() 面
面![]() ,所以面
,所以面![]() 的法向量为
的法向量为![]() ,再求出它们的夹角的余弦值.
,再求出它们的夹角的余弦值.
试题解析:(1)证明:设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() ,且
,且![]() 为
为![]() 中点,又
中点,又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)证明:因为四边形![]() 与
与![]() 均为菱形,
均为菱形,
所以![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)解:因为四边形![]() 为菱形,且
为菱形,且![]() ,所以△
,所以△![]() 为等边三角形,
为等边三角形,
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,故
,故![]() 平面
平面![]() .
.
由![]() ,
,![]() ,
,![]() 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系![]() .
.
设![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则有
,则有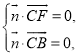 所以
所以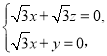
取![]() ,得
,得![]() .
.
易知平面![]() 的法向量为
的法向量为![]() .
.
由二面角![]() 是锐角,得
是锐角,得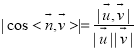
![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片。当初向各地作了广告推广,同时广告对销售收益也有影响。在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
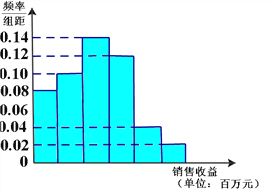
(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,并将各地销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元)
1
2
3
4
5
销售收益y(单位:百万元)
2
3
2
7
表中的数据显示,
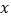 与
与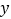 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算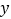 关于
关于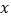 的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为
的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为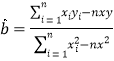 ,
,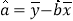 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆
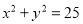 内”的概率.
内”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市有一块半径为40 m的半圆形绿化区域(以O 为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
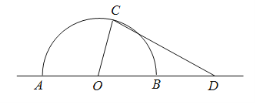
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,讨论
时,讨论 的单调性;
的单调性;(2)若对任意的
 ,
, ,
, 恒有
恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且
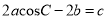 .
.(1)求角A的大小;
(2)若
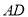 是
是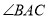 的角平分线,
的角平分线, 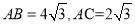 ,求
,求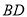 的长.
的长.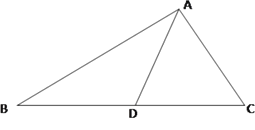
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
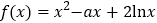 (其中
(其中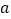 是实数)
是实数)(1)求
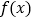 的单调区间;
的单调区间;(2)若设
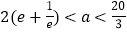 ,且
,且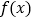 有两个极值点
有两个极值点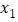 ,
,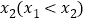 ,求
,求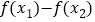 取值范围.(其中
取值范围.(其中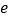 为自然对数的底数)
为自然对数的底数)
相关试题

