【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: 
(1)BE=EC;
(2)ADDE=2PB2 .
参考答案:
【答案】
(1)证明:连接OE,OA,则∠OAE=∠OEA,∠OAP=90°,
∵PC=2PA,D为PC的中点,
∴PA=PD,
∴∠PAD=∠PDA,
∵∠PDA=∠CDE,
∴∠OEA+∠CDE=∠OAE+∠PAD=90°,
∴OE⊥BC,
∴E是 ![]() 的中点,
的中点,
∴BE=EC;

(2)证明:∵PA是切线,A为切点,割线PBC与⊙O相交于点B,C,
∴PA2=PBPC,
∵PC=2PA,
∴PA=2PB,
∴PD=2PB,
∴PB=BD,
∴BDDC=PB2PB,
∵ADDE=BDDC,
∴ADDE=2PB2.
【解析】(1)连接OE,OA,证明OE⊥BC,可得E是 ![]() 的中点,从而BE=EC;(2)利用切割线定理证明PD=2PB,PB=BD,结合相交弦定理可得ADDE=2PB2 .
的中点,从而BE=EC;(2)利用切割线定理证明PD=2PB,PB=BD,结合相交弦定理可得ADDE=2PB2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, ⊥底面
⊥底面 ,
, 是
是 的中点.
的中点.已知
 ,
, ,
, ,
, .求:
.求:(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
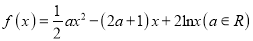 .
.(Ⅰ)求
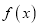 的单调区间;
的单调区间;(Ⅱ)设
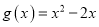 ,若对任意
,若对任意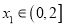 ,均存在
,均存在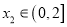 ,使得
,使得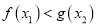 ,求
,求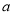 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,
 .
.
(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的首项
的首项 ,前
,前 项和为
项和为 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前n项和Tn,并证明:1≤Tn<
的前n项和Tn,并证明:1≤Tn< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
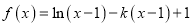 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
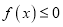 恒成立,试确定实数
恒成立,试确定实数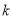 的取值范围;
的取值范围;(3)证明:
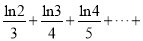
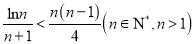 .
.
相关试题

