【题目】如图,在三棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
已知![]() ,
,![]() ,
,![]() ,
,![]() .求:
.求:
(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

参考答案:
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:(1)由题意结合三棱锥的体积公式可得三棱锥的体积为![]() ;
;
(2)取PB的中点E,连接DE,AE,则∠ADE(或其补角)是异面直线BC与AD所成的角.结合余弦定理计算可得异面直线BC与AD所成角的余弦值为![]() .
.
详解:
(1)S△ABC=![]() ×2×2
×2×2![]() =2
=2![]() ,三棱锥PABC的体积为V=
,三棱锥PABC的体积为V=![]() S△ABC·PA=
S△ABC·PA=![]() ×2
×2![]() ×2=
×2=![]() .
.
(2)取PB的中点E,连接DE,AE,则ED∥BC,
所以∠ADE(或其补角)是异面直线BC与AD所成的角.在△ADE中,DE=2,AE=![]() ,AD=2,cos∠ADE=
,AD=2,cos∠ADE=![]() =
=![]() .
.
故异面直线BC与AD所成角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面,
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.
其中真命题的个数是( ).
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱椎
 中,底面
中,底面 为菱形,
为菱形,  为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)若
 底面
底面 ,
,  ,
,  ,
,  ,求三棱椎
,求三棱椎 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知梯形
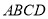 中,
中, 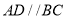 ,
, 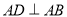 ,
, 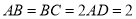 ,四边形
,四边形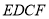 为矩形,
为矩形,  ,平面
,平面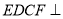 平面
平面 .
.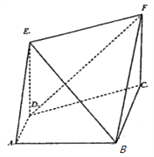
(Ⅰ)求证:
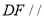 平面
平面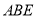 ;
;(Ⅱ)求平面
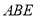 与平面
与平面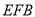 所成锐二面角的余弦值;
所成锐二面角的余弦值;(Ⅲ)在线段
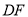 上是否存在点
上是否存在点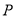 ,使得直线
,使得直线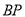 与平面
与平面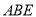 所成角的正弦值为
所成角的正弦值为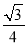 ,若存在,求出线段
,若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
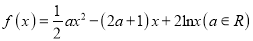 .
.(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)设
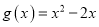 ,若对任意
,若对任意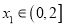 ,均存在
,均存在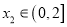 ,使得
,使得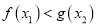 ,求
,求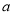 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:

(1)BE=EC;
(2)ADDE=2PB2 .
相关试题

