【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)圆心![]() 的轨迹
的轨迹![]() :
: ![]() ;
;
(2)![]() 和
和![]() 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为![]() ;
;
(3)当![]() 时,
时, ![]() 取最大值
取最大值![]() .
.
【解析】试题分析:(1)根据两圆相切得圆心距与半径之间关系: 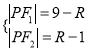 ,消去半径得
,消去半径得![]() ,符合椭圆定义,由定义可得轨迹方程(2)探究问题,实质是计算问题,即利用坐标求
,符合椭圆定义,由定义可得轨迹方程(2)探究问题,实质是计算问题,即利用坐标求![]() 和
和![]() 的比值:根据直线方程与椭圆方程联立方程组,利用两点间距离公式及韦达定理、弦长公式可得
的比值:根据直线方程与椭圆方程联立方程组,利用两点间距离公式及韦达定理、弦长公式可得![]() 和
和![]() 的表达式,两式相比即得比值
的表达式,两式相比即得比值![]() (3)因为
(3)因为![]() 的面积
的面积![]() 的面积,所以
的面积,所以![]() ,利用原点到直线距离得三角形的高,而底为弦长MN(2中已求),可得面积表达式,为一个分式函数,结合变量分离法(整体代换)、基本不等式求最值
,利用原点到直线距离得三角形的高,而底为弦长MN(2中已求),可得面积表达式,为一个分式函数,结合变量分离法(整体代换)、基本不等式求最值
试题解析:解:(1)设圆心![]() 的坐标为
的坐标为![]() ,半径为
,半径为![]() ,
,
由于动圆![]() 一圆
一圆![]() 相切,且与圆
相切,且与圆![]() 相内切,所以动圆
相内切,所以动圆![]() 与圆
与圆![]() 只能内切
只能内切
∴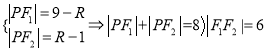
∴圆心![]() 的轨迹为以
的轨迹为以![]() 为焦点的椭圆,其中
为焦点的椭圆,其中![]() ,
,
∴![]()
故圆心![]() 的轨迹
的轨迹![]() .
.
(2)设![]() ,直线
,直线![]() ,则直线
,则直线![]() ,
,
由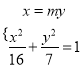 可得:
可得: 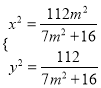 ,∴
,∴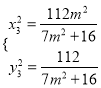 ,
,
∴![]()
由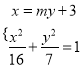 可得:
可得: ![]() ,
,
∴![]() ,
,
∴![]()
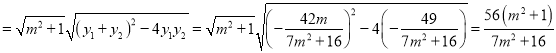 .
.
∴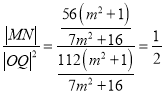
∴![]() 和
和![]() 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为![]() .
.
(3)∵![]() ,∴
,∴![]() 的面积
的面积![]() 的面积,∴
的面积,∴![]() ,
,
∵![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴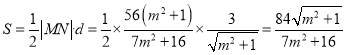 .1
.1
令![]() ,则
,则![]() ,
, 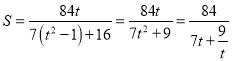 ,
,
∵![]() (当且仅当
(当且仅当![]() ,即
,即![]() ,亦即
,亦即![]() 时取等号)
时取等号)
∴当![]() 时,
时, ![]() 取最大值
取最大值![]() .1
.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
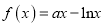 ,
, 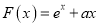 ,其中
,其中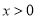 ,
, 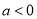 ,
,  为自然对数的底数.
为自然对数的底数. (Ⅰ)若
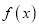 和
和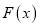 在区间
在区间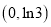 内具有相同的单调性,求实数
内具有相同的单调性,求实数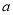 的取值范围;
的取值范围;(Ⅱ)若
 ,且函数
,且函数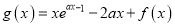 的最小值为
的最小值为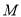 ,求
,求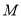 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与
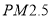 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与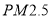 的数据如表:
的数据如表:时间
星期一
星期二
星期三
星期四
星期五
星期六
星期七
车流量
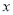 (万辆)
(万辆)1
2
3
4
5
6
7
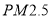 的浓度
的浓度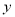 (微克/立方米)
(微克/立方米)28
30
35
41
49
56
62
(1)由散点图知
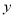 与
与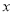 具有线性相关关系,求
具有线性相关关系,求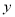 关于
关于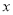 的线性回归方程;
的线性回归方程;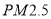 的浓度;
的浓度;(ii)规定:当一天内
 的浓度平均值在
的浓度平均值在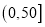 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内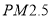 的浓度平均值在
的浓度平均值在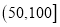 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
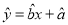 ,其中
,其中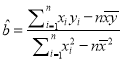 ,
, 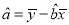 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设有两个命题:p:关于x的不等式x2+2x-4-a≥0对一切x∈R恒成立;q:已知a≠0,a≠±1,函数y=-|a|x在R上是减函数,若p∧q为假命题,p∨q为真命题,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列命题的否定,并判断其真假:
(1)p:末位数字为9的整数能被3整除;
(2)p:有的素数是偶数;
(3)p:至少有一个实数x,使x2+1=0;
(4)p:x,y∈R,x2+y2+2x-4y+5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:任意两个等边三角形都是相似的.
①它的否定是_________________________________________________________;
②否命题是_____________________________________________________________.
相关试题

