【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
参考答案:
【答案】![]() .
.
【解析】试题分析:利用一元二次不等式的解集与判别式的关系可化简p,利用三角函数两角和公式得sinx+cosx=![]() sin(x+
sin(x+![]() )∈[-
)∈[-![]() ,
, ![]() ],命题q:m≥
],命题q:m≥![]() .由于“命题p是真命题且命题q为假命题,即可得出.
.由于“命题p是真命题且命题q为假命题,即可得出.
试题解析:
对于命题p:
(1)当m-1=0时,原不等式化为2>0恒成立,满足题意.
(2)当m-1≠0时,只需![]()
得1<m<9,所以,m∈[1,9).
对于命题q:
sinx+cos x=![]() sin(x+
sin(x+![]() )∈[-
)∈[-![]() ,
,![]() ],若对于任意的x∈R,命题q:sin x+cos x>m是假命题,则m≥
],若对于任意的x∈R,命题q:sin x+cos x>m是假命题,则m≥![]() .
.
综上,m的取值范围是[![]() ,9).
,9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角梯形
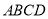 中,
中, 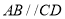 ,
, 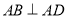 ,
, 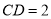 ,
, 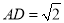 ,
, 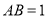 ,如图1所示,将
,如图1所示,将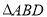 沿
沿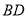 折起到
折起到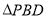 的位置,如图2所示.
的位置,如图2所示.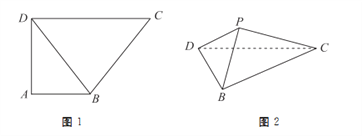
(1)当平面
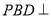 平面
平面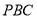 时,求三棱锥
时,求三棱锥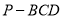 的体积;
的体积;(2)在图2中,
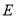 为
为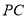 的中点,若线段
的中点,若线段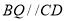 ,且
,且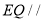 平面
平面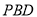 ,求线段
,求线段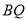 的长;
的长; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
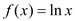 ,
, .
.(Ⅰ)若
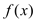 与
与 在
在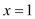 处相切,试求
处相切,试求 的表达式;
的表达式;(Ⅱ)若
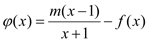 在
在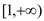 上是减函数,求实数
上是减函数,求实数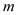 的取值范围;
的取值范围;(Ⅲ)证明不等式:
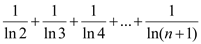
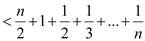 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人约定在中午12时到下午1时之间到某站乘公共汽车,又知这段时间内有4班公共汽车.设到站时间分别为12:15,12:30,12:45,1:00.如果他们约定:
①见车就乘;
②最多等一辆.
试分别求出在两种情况下两人同乘一辆车的概率.假设甲乙两人到达车站的时间是相互独立的,且每人在中午12点到1点的任意时刻到达车站是等可能的. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
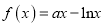 ,
, 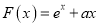 ,其中
,其中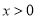 ,
, 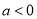 ,
,  为自然对数的底数.
为自然对数的底数. (Ⅰ)若
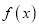 和
和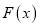 在区间
在区间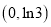 内具有相同的单调性,求实数
内具有相同的单调性,求实数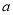 的取值范围;
的取值范围;(Ⅱ)若
 ,且函数
,且函数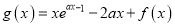 的最小值为
的最小值为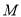 ,求
,求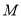 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与
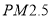 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与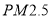 的数据如表:
的数据如表:时间
星期一
星期二
星期三
星期四
星期五
星期六
星期七
车流量
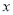 (万辆)
(万辆)1
2
3
4
5
6
7
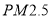 的浓度
的浓度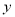 (微克/立方米)
(微克/立方米)28
30
35
41
49
56
62
(1)由散点图知
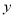 与
与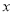 具有线性相关关系,求
具有线性相关关系,求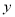 关于
关于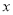 的线性回归方程;
的线性回归方程;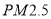 的浓度;
的浓度;(ii)规定:当一天内
 的浓度平均值在
的浓度平均值在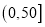 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内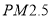 的浓度平均值在
的浓度平均值在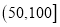 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
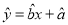 ,其中
,其中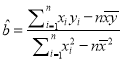 ,
, 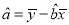 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
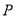 与圆
与圆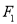 :
: 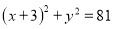 相切,且与圆
相切,且与圆 :
: 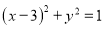 相内切,记圆心
相内切,记圆心 的轨迹为曲线
的轨迹为曲线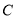 .设
.设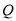 为曲线
为曲线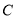 上的一个不在
上的一个不在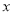 轴上的动点,
轴上的动点, 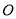 为坐标原点,过点
为坐标原点,过点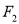 作
作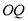 的平行线交曲线
的平行线交曲线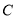 于
于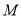 ,
, 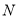 两个不同的点.
两个不同的点.(Ⅰ)求曲线
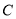 的方程;
的方程;(Ⅱ)试探究
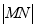 和
和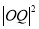 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;(Ⅲ)记
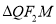 的面积为
的面积为 ,
, 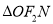 的面积为
的面积为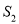 ,令
,令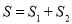 ,求
,求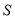 的最大值.
的最大值.
相关试题

