【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中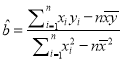 ,
, ![]() .
.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)
;(Ⅱ)(ⅰ)![]() 微克/立方米;(ⅱ)控制当天车流量在
微克/立方米;(ⅱ)控制当天车流量在![]() 万辆以内.
万辆以内.
【解析】试题分析:(Ⅰ)由表中数据先计算![]() ,代入公式
,代入公式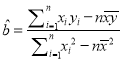 求出
求出![]() ,由
,由![]() 求出
求出![]() 即可得出线性回归方程;(Ⅱ)(ⅰ)由(Ⅰ)中公式,令
即可得出线性回归方程;(Ⅱ)(ⅰ)由(Ⅰ)中公式,令![]() 计算即可;(ⅱ)解不等式
计算即可;(ⅱ)解不等式![]() 即可.
即可.
试题解析: (Ⅰ)由数据可得: ![]() ,………(1分)
,………(1分)
![]() ,(2分)
,(2分)
![]() ,
, ![]() ,……(4分)
,……(4分)
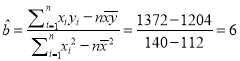 ,…………(6分)
,…………(6分)
![]() …………(7分)
…………(7分)
故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .……(8分)
.……(8分)
(Ⅱ)(ⅰ)当车流量为![]() 万辆时,即
万辆时,即![]() 时,
时, ![]() .
.
故车流量为![]() 万辆时,
万辆时, ![]() 的浓度为
的浓度为![]() 微克/立方米.(10分)
微克/立方米.(10分)
(ⅱ)根据题意信息得: ![]() ,即
,即![]() ,…(11分)
,…(11分)
故要使该市某日空气质量为优或为良,则应控制当天车流量在![]() 万辆以内.……(12分)
万辆以内.……(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次抽样调查中测得样本的6组数据,得到一个变量
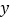 关于
关于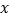 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表: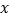
2
3
4
5
6
7
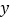
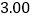
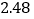
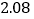
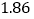
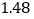
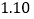
(1)请用相关系数
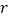 加以说明
加以说明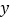 与
与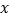 之间存在线性相关关系(当
之间存在线性相关关系(当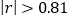 时,说明
时,说明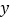 与
与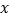 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
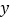 关于
关于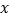 的回归方程并预测当
的回归方程并预测当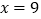 时,对应的
时,对应的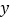 值为多少(
值为多少(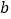 精确到
精确到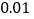 ).
).附参考公式:回归方程
 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: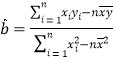 ,
,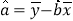 ,相关系数
,相关系数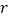 公式为:
公式为: .
.参考数据:
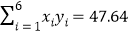 ,
,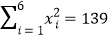 ,
,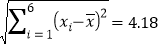 ,
,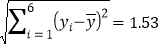 .
. -
科目: 来源: 题型:
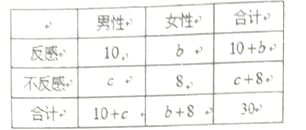
查看答案和解析>>【题目】“中国式过马路” 存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的
 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是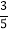 .
.(1)求
 列联表中的
列联表中的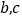 的值;
的值;
(2)根据列联表中的数据,判断是否有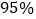 把握认为反感“中国式过马路”与性别有关?
把握认为反感“中国式过马路”与性别有关?参考公式:
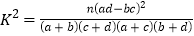 ,
,
临界值表:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂需要确定加工某大型零件所花费的时间,连续4天做了4次统计,得到的数据如下:
零件的个数
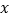 (个)
(个)2
3
4
5
加工的时间
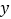 (小时)
(小时)2.5
3
4
5.5
(1)在直角坐标系中画出以上数据的散点图,求出
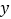 关于
关于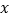 的回归方程
的回归方程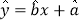 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线; 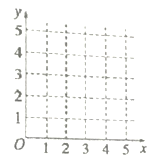
(2)试预测加工10个零件需要多少时间?
参考公式:两个具有线性关系的变量的一组数据:
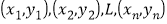 ,
,其回归方程为
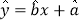 ,其中
,其中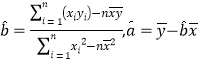
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
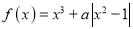 ,
, 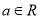 ,则对于不同的实数
,则对于不同的实数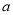 ,函数
,函数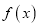 的单调区间个数不可能是( )
的单调区间个数不可能是( )A. 1个 B. 2个 C. 3个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满足100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组
频数
频率
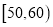
5
0.05
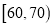
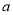
0.20
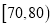
35
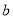
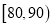
25
0.25
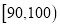
15
0.15
合计
100
1.00
(1)求
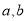 的值及随机抽取一考生恰为优秀生的概率;
的值及随机抽取一考生恰为优秀生的概率;(2)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(3)在第(2)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在
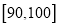 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁)
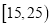
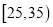
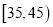
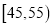
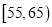
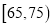
频数
5
10
15
10
5
5
赞成人数
5
10
12
7
2
1
(1)由以上统计数据填写下面
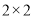 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;年龄不低于45岁的人
年龄低于45岁的人
合计
赞成
不赞成
合计
(2)若对年龄分别在
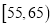 ,
, 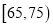 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.参考公式:
 ,其中
,其中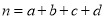
参考数据:
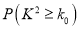
0.050
0.010
0.001
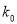
3.841
6.635
10.828
相关试题

