【题目】如图,四棱柱![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,
的中点,![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,写出相应点的坐标,即可通过线面垂直的判定方法证得
,写出相应点的坐标,即可通过线面垂直的判定方法证得![]() 平面
平面![]() ;
;
(2)写出相应点的坐标,求出平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量,即可求得答案.
的一个法向量,即可求得答案.
详解:(1)证明方法一: 连接![]() ,因为底面
,因为底面![]() 是等腰梯形且
是等腰梯形且![]()
所以,![]() ,又因为
,又因为![]() 是
是![]() 的中点,
的中点,
因此,![]() 且
且![]() ,
,
所以,![]() 且
且![]() ,
,
又因为![]() 且
且![]() ,
,
所以![]() ,
,
因为,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以,平面![]() 平面
平面![]() ,
,
在平行四边形![]() 中,因为
中,因为![]() ,
,
所以平行四边形![]() 是菱形,
是菱形,
因此![]() ,
,
所以![]() 平面
平面![]() .
.
解法二:底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,
所以,![]() ,
,
因此![]() ,
,
以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因此![]() ,且
,且![]() ,
,
所以![]() 且
且![]() ,
,
所以,![]() 平面
平面![]() .
.

(2)底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,
所以,![]() ,
,
因此![]() ,
,
以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,
,![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
由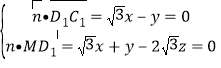 得
得![]() ,
,
由![]() 是平面
是平面![]() 的法向量,
的法向量,
因此![]() ,
,
平面![]() 和平面
和平面![]() 所成的锐二面角的余弦值是
所成的锐二面角的余弦值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点
 为坐标原点,椭圆
为坐标原点,椭圆 :
: 的右顶点为
的右顶点为 ,上顶点为
,上顶点为 ,过点
,过点 且斜率为
且斜率为 的直线与直线
的直线与直线 相交于点
相交于点 ,且
,且 .
.(1)求椭圆
 的离心率
的离心率 ;
;(2)
 是圆
是圆 :
: 的一条直径,若椭圆
的一条直径,若椭圆 经过
经过 ,
, 两点,求椭圆
两点,求椭圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
 ,则A∩(RB)等于( )
,则A∩(RB)等于( )
A.(﹣∞,1)
B.(0,4)
C.(0,1)
D.(1,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 ),
), 为自然对数的底数.
为自然对数的底数.(Ⅰ)当
 时,求函数
时,求函数 在区间
在区间 上的最大值;
上的最大值;(Ⅱ)若函数
 只有一个零点,求
只有一个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图的算法框图,输出的结果S的值为( )

A.
B.0
C.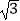
D.-
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b在区间
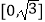 上取值,则函数
上取值,则函数 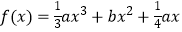 在R上有两个相异极值点的概率是( )
在R上有两个相异极值点的概率是( )
A.
B.1-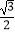
C.
D.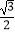
相关试题

