【题目】设集合 ![]() ,则A∩(RB)等于( )
,则A∩(RB)等于( )
A.(﹣∞,1)
B.(0,4)
C.(0,1)
D.(1,4)
参考答案:
【答案】C
【解析】解:当x>0时,A中不等式变形得x<1,此时0<x<1;
当x<0时,A中不等式变形得:x>1,此时无解,
∴A=(0,1),
由B中y= ![]() ,得到2x﹣16≥0,即2x≥24 ,
,得到2x﹣16≥0,即2x≥24 ,
解得:x≥4,即B=[4,+∞),
∴RB=(﹣∞,4),
则A∩(RB)=(0,1),
故选:C.
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案,需要熟知求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知海岛
 在海岛
在海岛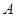 北偏东
北偏东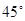 ,
,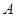 ,
, 相距
相距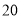 海里,物体甲从海岛
海里,物体甲从海岛 以
以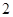 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛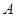 移动,同时物体乙从海岛
移动,同时物体乙从海岛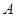 沿着海岛
沿着海岛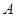 北偏西
北偏西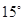 方向以
方向以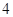 海里/小时的速度移动.
海里/小时的速度移动.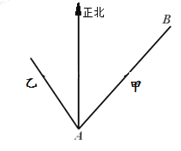
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛
 到达海岛
到达海岛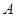 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
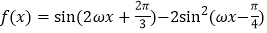 ,
, .
.(1)当
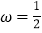 时,求函数
时,求函数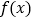 的单调递增区间;
的单调递增区间;(2)对于
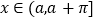 ,
,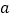 为任意实数,关于
为任意实数,关于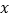 的方程
的方程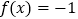 恰好有两个不等实根,求实数
恰好有两个不等实根,求实数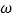 的值;
的值;(3)在(2)的条件下,若不等式
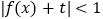 在
在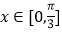 恒成立,求实数
恒成立,求实数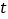 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
 为坐标原点,椭圆
为坐标原点,椭圆 :
: 的右顶点为
的右顶点为 ,上顶点为
,上顶点为 ,过点
,过点 且斜率为
且斜率为 的直线与直线
的直线与直线 相交于点
相交于点 ,且
,且 .
.(1)求椭圆
 的离心率
的离心率 ;
;(2)
 是圆
是圆 :
: 的一条直径,若椭圆
的一条直径,若椭圆 经过
经过 ,
, 两点,求椭圆
两点,求椭圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 ),
), 为自然对数的底数.
为自然对数的底数.(Ⅰ)当
 时,求函数
时,求函数 在区间
在区间 上的最大值;
上的最大值;(Ⅱ)若函数
 只有一个零点,求
只有一个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点,
的中点, 平面
平面 .
.
(1)求证:
 平面
平面 ;
;(2)若
 ,求平面
,求平面 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

