【题目】若a,b在区间 ![]() 上取值,则函数
上取值,则函数 ![]() 在R上有两个相异极值点的概率是( )
在R上有两个相异极值点的概率是( )
A.![]()
B.1- ![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:易得f′(x)=ax2+2bx+ ![]() a,
a,
函数f(x)在R上有两个相异极值点的充要条件:
是a≠0且其导函数的判别式大于0,即a≠0且4b2﹣a2>0,
又a,b在区间[0, ![]() ]上取值,则a>0,b>
]上取值,则a>0,b> ![]() a,
a,
点(a,b)满足的区域如图中阴影部分所示,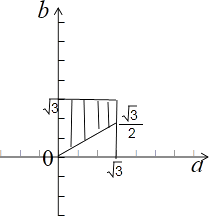
其中正方形区域的面积为3,
阴影部分的面积为3﹣ ![]() =
= ![]() ,
,
故所求的概率p= ![]() =
= ![]() ,
,
故选:C.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点,
的中点, 平面
平面 .
.
(1)求证:
 平面
平面 ;
;(2)若
 ,求平面
,求平面 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图的算法框图,输出的结果S的值为( )

A.
B.0
C.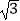
D.-
-
科目: 来源: 题型:
查看答案和解析>>【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是
 ,样本数据分组为
,样本数据分组为 .
.
(1)求直方图中
 的值;
的值;(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用
 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
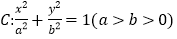 的离心率为
的离心率为 ,
,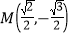 是椭圆上一点.
是椭圆上一点.(1)求椭圆的标准方程;
(2)过椭圆右焦点
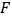 的直线与椭圆交于
的直线与椭圆交于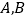 两点,
两点,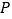 是直线
是直线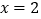 上任意一点.证明:直线
上任意一点.证明:直线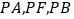 的斜率成等差数列.
的斜率成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程
 ,其中
,其中 ,
, .
.(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
相关试题

