【题目】已知函数![]() (
(![]() 且
且![]() ),
),![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅱ)若函数![]() 只有一个零点,求
只有一个零点,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(1)由导函数的解析式可得![]() .
.
(2)由![]() ,得
,得![]() ,分类讨论
,分类讨论![]() 和
和![]() 两种情况可得
两种情况可得![]() .
.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() ,令
,令![]() ,解得
,解得![]() ,
,
![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,
∴![]() ,而
,而![]() ,
, ![]() ,
,
即![]() .
.
(Ⅱ)![]() ,
, ![]() ,
,
令![]() ,得
,得![]() ,则
,则
①当![]() 时,
时, ![]() ,
,
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以当![]() 时,
时, ![]() 有最小值
有最小值![]() ,
,
因为函数![]() 只有一个零点,且当
只有一个零点,且当![]() 和
和![]() 时,都有
时,都有![]() ,则
,则![]() ,即
,即![]() ,
,
因为当![]() 时,
时, ![]() ,所以此方程无解.
,所以此方程无解.
②当![]() 时,
时, ![]() ,
,
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以当![]() 时,
时, ![]() 有最小值
有最小值![]() ,
,
因为函数![]() 只有一个零点,且当
只有一个零点,且当![]() 和
和![]() 时,都有
时,都有![]() ,
,
所以![]() ,即
,即![]() (
(![]() )(*)
)(*)
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
所以当![]() 时,
时, ![]() ,所以方程(*)有且只有一解
,所以方程(*)有且只有一解![]() .
.
综上, ![]() 时函数
时函数![]() 只有一个零点.
只有一个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ,求使得不等式
,求使得不等式  恒成立的实数k的取值范围.
恒成立的实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是自然对数的底数,
是自然对数的底数,  ,
,  ,
,  ,
,  .
.(1)设
 ,求
,求 的极值;
的极值;(2)设
 ,求证:函数
,求证:函数 没有零点;
没有零点;(3)若
 ,设
,设 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱柱
 中,点
中,点 分别为
分别为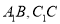 的中点.
的中点.
(1)求证:
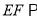 平面
平面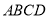 ;
;(2)若四棱柱
 是长方体,且
是长方体,且 ,求平面
,求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
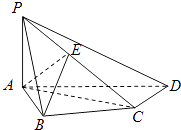
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=log
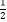 (x2﹣2x)的单调递增区间是( )
(x2﹣2x)的单调递增区间是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,0)
D.(﹣∞,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在
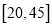 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.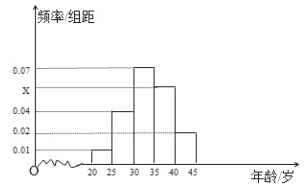
(Ⅰ)求图中
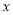 的值;
的值;(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为
 ,求
,求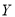 的分布列及数学期望.
的分布列及数学期望.
相关试题

