【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
参考答案:
【答案】(1) f(1)=0;(2)见解析.(3){x|-15<x<17且x≠1}.
【解析】试题分析:(1)抽象函数求具体指,用赋值法;(2)根据定义求证函数的奇偶性找f(-x)和f(x)的关系;(3)先利用f(4×4)=f(4)+f(4)=2得到f(x-1)<2f(|x-1|)<f(16).再根据单调性列出不等式求解即可.
(1)∵对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2),
∴令x1=x2=1,得f(1)=2f(1),∴f(1)=0.
(2)令x1=x2=-1,有f(1)=f(-1)+f(-1),∴f(-1)=![]() f(1)=0.
f(1)=0.
令x1=-1,x2=x有f(-x)=f(-1)+f(x),∴f(-x)=f(x),∴f(x)为偶函数.
(3)依题设有f(4×4)=f(4)+f(4)=2,
由(2)知,f(x)是偶函数,∴f(x-1)<2f(|x-1|)<f(16).又f(x)在(0,+∞)上是增函数.∴0<|x-1|<16,解之得-15<x<17且x≠1.
∴x的取值范围是{x|-15<x<17且x≠1}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. 当
当 时,试判断函数
时,试判断函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明; 若不等式
若不等式 在
在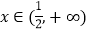 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△A1B1C1的三内角余弦值分别等于△A2B2C2三内角的正弦值,那么两个三角形六个内角中的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图像经过点
的图像经过点 ,且满足
,且满足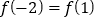 ,
,(1)求
 的解析式;
的解析式;(2)已知
 ,求函数
,求函数 在
在 的最大值和最小值;
的最大值和最小值;函数
 的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由
的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱ABC﹣A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C﹣ABB1A1的体积等于4.

(1)求AA1的值;
(2)求C1到平面A1B1C的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知函数f(x)=

(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:
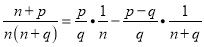 ,已知数列
,已知数列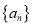 中,
中, 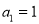 ,
, 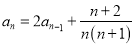
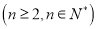 ,则数列
,则数列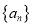 的通项公式
的通项公式 __________.
__________.
相关试题

