【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量![]() =(1,bn),
=(1,bn), ![]() =(an-1,Sn),
=(an-1,Sn), ![]() //
//![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若![]() ,
, ![]() =0.
=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得![]() 成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() .
.
【解析】试题分析:(1)利用两个向量平行的坐标关系得到Sn=(an-1)bn,进一步对n取值,得到数列{an}是等差数列;(2)①由bn=![]() ,则2Sn=nan-n③,又2Sn+1=(n+1)an+1-(n+1)④,两式相减即可得到数列{an}的递推公式,进一步对n 取值,得到数列{an}是首项为-1,公差为1的等差数列.
,则2Sn=nan-n③,又2Sn+1=(n+1)an+1-(n+1)④,两式相减即可得到数列{an}的递推公式,进一步对n 取值,得到数列{an}是首项为-1,公差为1的等差数列.
②由①得到数列{cn}通项公式,根据m,l的范围讨论可能的取值.
试题解析:(1)因为![]() =(1,bn),
=(1,bn), ![]() =(an-1,Sn),
=(an-1,Sn), ![]() //
//![]()
得Sn=(an1)bn,当bn=2,则Sn=2an2①,
当n=1时,S1=2a12,即a1=2,
又Sn+1=2an+12②,
②①得Sn+1Sn=2an+12an,
即an+1=2an,又a1=2,
所以{an}是首项为2,公比为2的等比数列,
所以an=2n.…(4分)
(2)①证明:因为bn=n2,则2Sn=nann③,
当n=1时,2S1=a11,即a1=1,
又2Sn+1=(n+1)an+1(n+1)④,
④③得
2Sn+12Sn=(n+1)an+1nan1,
即(n1)an+1nan1=0⑤,
又nan+2(n+1)an+11=0⑥
⑥⑤得,nan+22nan+1+nan=0,
即an+2+an=2an+1,所以数列{an}是等差数列
②又a1=1,a2=0,
所以数列{an}是首项为1,公差为1的等差数列。
an=1+(n1)×1=n2,所以cn=n+1n,…(10分)
假设存在l<m(l≠2,m≠2),使得cl、c2、cm成等比数列,即c22=clcm,
可得94=l+1lm+1m,
整理得5lm4l=4m+4即l=4m+45m4,由4m+45m41,得1m8
由![]() <m,所以存在
<m,所以存在![]() =1,m=8符合条件
=1,m=8符合条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】《选修4—4:坐标系与参数方程》
已知直线l的参数方程为
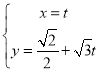 (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).(1)求直线l的倾斜角和曲线
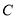 的直角坐标方程;
的直角坐标方程;(2)若直线l与曲线C交于A,B两点,设点
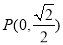 ,求
,求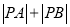 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 为圆
为圆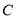 上任一点.
上任一点.(1)求
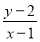 的最大值与最小值;
的最大值与最小值;(2)求
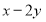 的最大值与最小值.
的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】牛大叔常说“价贵货不假”,他这句话的意思是:“不贵”是“假货”的( )
A.充分条件B.必要条件C.充分必要条件D.既非充分也非必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁)
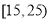
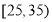
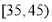
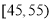
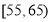
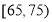
频数
5
10
15
10
5
5
赞成人数
3
10
12
7
2
1
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的
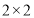 列联表,并判断是否有
列联表,并判断是否有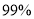 的把握认为“使用微信交流”的态度与人的年龄有关:
的把握认为“使用微信交流”的态度与人的年龄有关:年龄不低于45岁的人数
年龄低于45岁的人数
合计
赞成
不赞成
合计
(2)若从年龄在
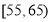 ,
,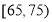 的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为
的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为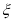 ,求随机变量
,求随机变量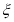 的分布列及数学期望.
的分布列及数学期望.参考数据如下:
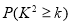
0.050
0.010
0.001
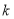
3.841
6.635
10.828
参考公式:
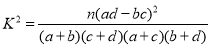 ,
,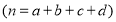 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(
 ,
, ),记∠COA=α.
),记∠COA=α.
(Ⅰ)求
 的值;
的值;(Ⅱ)求cos∠COB的值.
相关试题

