【题目】已知圆![]() 为圆
为圆![]() 上任一点.
上任一点.
(1)求![]() 的最大值与最小值;
的最大值与最小值;
(2)求![]() 的最大值与最小值.
的最大值与最小值.
参考答案:
【答案】(1)最大值是![]() ,最小值是
,最小值是![]() ;(2)最大值是
;(2)最大值是![]() ,最小值是
,最小值是![]() .
.
【解析】
(2)试题分析:(1)![]() 是圆上的点与点
是圆上的点与点![]() 连线的斜率,最大、最小值分别是过点
连线的斜率,最大、最小值分别是过点![]() 的圆
的圆![]() 的两条切线的斜率.设切线的斜率为
的两条切线的斜率.设切线的斜率为![]() ,利用圆心到直线的距离等于半径,求出斜率
,利用圆心到直线的距离等于半径,求出斜率![]() ;(2)令
;(2)令![]() ,则
,则![]() ,转化为线性规划问题求解,平移直线
,转化为线性规划问题求解,平移直线![]() ,当直线和圆
,当直线和圆![]() 有公共点时,
有公共点时,![]() 的范围即可确定,且最值在直线与圆相切时取得.利用点到直线的距离公式,求得
的范围即可确定,且最值在直线与圆相切时取得.利用点到直线的距离公式,求得![]() 的取值范围.
的取值范围.
试题解析:
(1)显然![]() 可以看作是点与点连线的斜率.令
可以看作是点与点连线的斜率.令![]() ,如图所示,则其最大、最小值分别是过点
,如图所示,则其最大、最小值分别是过点![]() 的圆
的圆![]() 的两条切线的斜率.
的两条切线的斜率.
对上式整理得![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() .
.
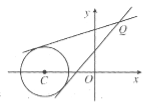
(3)令![]() ,则
,则![]() 可视为一组平行线,当直线和圆
可视为一组平行线,当直线和圆![]() 有公共点时,
有公共点时,![]() 的范围即可确定,且最值在直线与圆相切时取得.
的范围即可确定,且最值在直线与圆相切时取得.
依题意,得![]() ,取得
,取得![]() ,
,
故![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设计一份学生食堂饭菜质量、饭菜价格、服务质量满意程度的调查问卷.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
 (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.(Ⅰ)求在未来4年中,至多1年的年入流量超过120的概率;
(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
 限制,并有如下关系;
限制,并有如下关系;年入流量




发电机最多可运行台数
1
2
3
若某台发电机运行,则该台发电机年利润为5000万元;若某台发电机未运行,则该台发电机年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】《选修4—4:坐标系与参数方程》
已知直线l的参数方程为
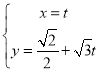 (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).(1)求直线l的倾斜角和曲线
 的直角坐标方程;
的直角坐标方程;(2)若直线l与曲线C交于A,B两点,设点
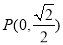 ,求
,求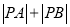 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】牛大叔常说“价贵货不假”,他这句话的意思是:“不贵”是“假货”的( )
A.充分条件B.必要条件C.充分必要条件D.既非充分也非必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量
 =(1,bn),
=(1,bn),  =(an-1,Sn),
=(an-1,Sn),  //
// .
.(1)若bn=2,求数列{an}通项公式;
(2)若
 ,
,  =0.
=0.①证明:数列{an}为等差数列;
②设数列{cn}满足
 ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得 成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
成等比数列,若存在,求出l、m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域.
相关试题

