【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用微信交流”的态度与人的年龄有关:
的把握认为“使用微信交流”的态度与人的年龄有关:
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为
的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:![]() ,
,![]() .
.
参考答案:
【答案】(1)有![]() 的把握(2)分布列见解析,
的把握(2)分布列见解析,![]()
【解析】
试题分析:(1)根据数据填表,再根据卡方公式求卡方系数:![]() ,对照比较,确定有无把握(2)先确定随机变量可能取法:0,1,2,3,再利用组合数求对应概率,列表得分布列,最后根据公式求数学期望:总事件数为
,对照比较,确定有无把握(2)先确定随机变量可能取法:0,1,2,3,再利用组合数求对应概率,列表得分布列,最后根据公式求数学期望:总事件数为![]() ,对应事件数分别为
,对应事件数分别为![]() ,
,![]() ;
;![]() ,
,![]()
试题解析:(1)![]() 列联表
列联表
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | 3 | 32 | 35 |
不赞成 | 7 | 8 | 15 |
合计 | 10 | 40 | 50 |
![]() ,
,
所以有![]() 的把握认为“使用微信交流”的态度与人的年龄有关.
的把握认为“使用微信交流”的态度与人的年龄有关.
(2)![]() 所有可能取值有0,1,2,3,
所有可能取值有0,1,2,3,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
所以![]() 的分布列是
的分布列是
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的期望值是
的期望值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】牛大叔常说“价贵货不假”,他这句话的意思是:“不贵”是“假货”的( )
A.充分条件B.必要条件C.充分必要条件D.既非充分也非必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量
 =(1,bn),
=(1,bn),  =(an-1,Sn),
=(an-1,Sn),  //
// .
.(1)若bn=2,求数列{an}通项公式;
(2)若
 ,
,  =0.
=0.①证明:数列{an}为等差数列;
②设数列{cn}满足
 ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得 成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
成等比数列,若存在,求出l、m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(
 ,
, ),记∠COA=α.
),记∠COA=α.
(Ⅰ)求
 的值;
的值;(Ⅱ)求cos∠COB的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
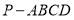 中,
中,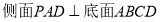 ,侧棱
,侧棱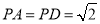 ,底面
,底面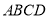 为直角梯形,其中
为直角梯形,其中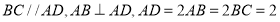 ,
,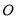 为
为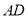 中点.
中点.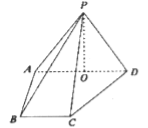
(1)求证:
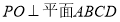 ;
;(2)求异面直线
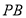 与
与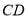 所成角的余弦值;
所成角的余弦值;(3)线段
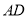 上是否存在
上是否存在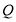 ,使得它到平面
,使得它到平面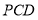 的距离为
的距离为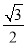 ?若存在,求出
?若存在,求出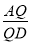 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
相关试题

