【题目】
已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(1)根据使函数的解析式有意义的原则,构造关于自变量![]() 的不等式组,即可求解函数的定义域;
的不等式组,即可求解函数的定义域;
(2)利用对数函数的运算性质,化简函数的解析式,并根据二次函数的图象与性质,可分析出函数的最小值为![]() 时,即可求解实数
时,即可求解实数![]() 的值.
的值.
(3)若不等式![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,设出新函数
上恒成立,设出新函数![]() ,利用基本不等式求解最大值,即可求解实数
,利用基本不等式求解最大值,即可求解实数![]() 的取值范围.
的取值范围.
详解:(1)要使函数有意义:则有![]() ,解得-2<x<1
,解得-2<x<1
∴ 函数的定义域![]() 为
为![]()
(2)![]()
因为 ![]()
所以 ![]()
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
由![]() ,得
,得![]() ,
,
(3)由![]() 在
在![]() 恒成立,
恒成立,
得 ![]()
因为![]() ,所以
,所以![]()
所以![]() 在
在![]() 恒成立
恒成立
设![]() ,令
,令![]()
则![]()
即![]() ,因为
,因为![]() ,
,
所以![]() (当且仅当
(当且仅当![]() 时,取等号
时,取等号
所以![]()
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】对两个变量x , y进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本点的中心
必过样本点的中心 
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动,得到如下的列联表:
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
由
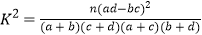 计算得
计算得 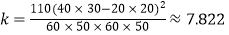
附表:P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C.有99%以上的把握认为“爱好该项运动与性别无关”
D.有99%以上的把握认为“爱好该项运动与性别有关” -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
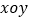 中,曲线C的参数方程为
中,曲线C的参数方程为 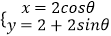 (
( 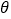 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 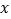 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)写出曲线C的极坐标方程;
(2)设点M的极坐标为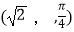 ,过点M的直线
,过点M的直线 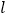 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若 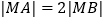 ,求
,求 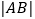 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知等差数列
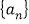 ,
, 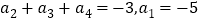 .
.(1)求数列
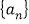 的通项公式;
的通项公式;(2)记数列
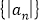 的前
的前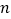 项和为
项和为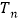 ,求
,求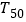 ;
;(3)是否存在正整数
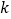 ,使得
,使得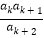 仍为数列
仍为数列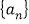 中的项,若存在,求出所有满足的正整数
中的项,若存在,求出所有满足的正整数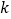 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在一个圆形的六个区域种植观赏植物,要求同一块中种植同一种植物,相邻的两块种植不同的植物,现有4种不同的植物可供选择,则有几种种植方案?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店
A店
B店
C店
售价x(元)
80
86
82
88
84
90
销量y(件)
88
78
85
75
82
66
(1)分别以三家连锁店的平均售价与平均销量为散点,求出售价与销量的回归直线方程 ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附:
相关试题

