【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
参考答案:
【答案】
(1)解:由于月产量为x台,则总成本为20000+100x,
从而利润f(x)= 
(2)解:当0≤x≤400时,f(x)=300x﹣ ![]() ﹣20000=﹣
﹣20000=﹣ ![]() (x﹣300)2+25000,
(x﹣300)2+25000,
∴当x=300时,有最大值25000;
当x>400时,f(x)=60000﹣100x是减函数,
∴f(x)=60000﹣100×400<25000.
∴当x=300时,有最大值25000,
即当月产量为300台时,公司所获利润最大,最大利润是25000元
【解析】(1)根据利润=收益﹣成本,由已知分两段当0≤x≤400时,和当x>400时,求出利润函数的解析式;(2)根据分段函数的表达式,分别求出函数的最大值即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, ,
, ,
, ,
, ,
, 分别为
分别为 的中点,
的中点, .
.
(1)求证:平面
 平面
平面 ;
;(2)设
 ,若平面
,若平面 与平面
与平面 所成锐二面角
所成锐二面角 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
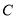 :
: 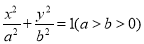 的离心率为
的离心率为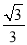 ,过右焦点
,过右焦点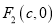 垂直于
垂直于 轴的直线与椭圆交于
轴的直线与椭圆交于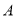 ,
,  两点且
两点且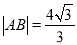 ,又过左焦点
,又过左焦点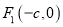 任作直线
任作直线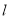 交椭圆于点
交椭圆于点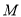 .
.(Ⅰ)求椭圆
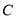 的方程;
的方程;(Ⅱ)椭圆
 上两点
上两点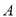 ,
, 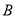 关于直线
关于直线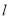 对称,求
对称,求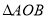 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(ax﹣1)(x﹣1).
(1)若不等式f(x)<0的解集为{x|1<x<2},求实数a的值;
(2)当a>0时,解关于x的不等式f(x)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】在区间
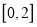 上任取两个实数
上任取两个实数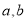 ,则函数
,则函数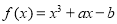 在区间
在区间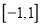 上有且只有一个零点的概率是
上有且只有一个零点的概率是A.
 B.
B.  C.
C. 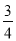 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0)时f(x)=(
 )x , 则 f(log28)等于( )
)x , 则 f(log28)等于( )
A.3
B.
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是等差数列,下列结论中正确的是( )
A.若a1+a2>0,则a2+a3>0
B.若a1+a3<0,则a1+a2<0
C.若0<a1<a2 , 则a2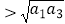
D.若a1<0,则(a2﹣a1)(a2﹣a3)>0
相关试题

