【题目】在区间![]() 上任取两个实数
上任取两个实数![]() ,则函数
,则函数![]() 在区间
在区间![]() 上有且只有一个零点的概率是
上有且只有一个零点的概率是
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
参考答案:
【答案】D
【解析】本试题主要是考查了几何概型的运用。对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果。
由题意知本题是一个几何概型,∵a∈[0,2],∴f'(x)=3x2+a≥0,∴f(x)是增函数若f(x)在[-1,1]有且仅有一个零点,则f(-1)f(1)≤0∴(-1-a-b)(1+a-b)≤0,即(1+a+b)(1+a-b)≥0由线性规划内容知全部事件的面积为2×2=4,满足条件的面积4-![]() ×1×1=
×1×1=![]() ,故选D.
,故选D.
解决该试题的关键是根据所给的条件很容易做出试验发生包含的事件对应的面积,而满足条件的事件是函数f(x)=x3+ax-b在区间[-1,1]上有且仅有一个零点,求出导函数,看出函数是一个增函数,有零点等价于在自变量区间的两个端点处函数值符号相反,得到条件,做出面积,根据几何概型概率公式得到结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
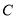 :
: 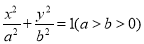 的离心率为
的离心率为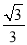 ,过右焦点
,过右焦点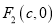 垂直于
垂直于 轴的直线与椭圆交于
轴的直线与椭圆交于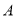 ,
,  两点且
两点且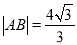 ,又过左焦点
,又过左焦点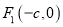 任作直线
任作直线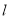 交椭圆于点
交椭圆于点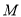 .
.(Ⅰ)求椭圆
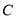 的方程;
的方程;(Ⅱ)椭圆
 上两点
上两点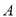 ,
, 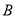 关于直线
关于直线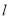 对称,求
对称,求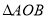 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(ax﹣1)(x﹣1).
(1)若不等式f(x)<0的解集为{x|1<x<2},求实数a的值;
(2)当a>0时,解关于x的不等式f(x)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=
 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0)时f(x)=(
 )x , 则 f(log28)等于( )
)x , 则 f(log28)等于( )
A.3
B.
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是等差数列,下列结论中正确的是( )
A.若a1+a2>0,则a2+a3>0
B.若a1+a3<0,则a1+a2<0
C.若0<a1<a2 , 则a2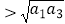
D.若a1<0,则(a2﹣a1)(a2﹣a3)>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
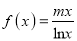 ,曲线
,曲线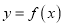 在点
在点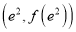 处的切线与直线
处的切线与直线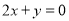 垂直(其中
垂直(其中 为自然对数的底数).
为自然对数的底数).(1)求
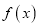 的解析式及单调递减区间;
的解析式及单调递减区间;(2)是否存在常数
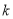 ,使得对于定义域内的任意
,使得对于定义域内的任意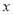 ,
, 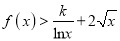 恒成立,若存在,求出
恒成立,若存在,求出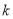 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

