【题目】有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
参考答案:
【答案】(1)![]() ; (2)
; (2) ![]()
【解析】
试题分析:(1)本题中不仅要选出5名医生(元素),还要求分配到5个地区(空位),因此是一道“既选又排”的排列组合综合问题,解决这类问题的方法是“先选后排”,同时要注意特殊元素、特殊位置优先安排的原则。
(2)首先将分成以下两类情况第一类:一组中女医生1人,男医生4人,另一组中女医生3人,男医生2人;第二类:两组中人数都有女医生2人男医生3人;最后将这两组医生分派到两地去,并且每组选出正副组长两人,是排列问题.
(1)分三步完成.
第一步:从6名男医生中选3名有![]() 种方法;
种方法;
第二步:从4名女医生中选2名有![]() 种方法;
种方法;
第三步:对选出的5人分配到5个地区有A种方法.
根据分步乘法计数原理,共有![]() (种).
(种).
(2)医生的选法有以下两类情况:
第一类:一组中女医生1人,男医生4人,另一组中女医生3人,男医生2人.共有![]() 种不同的分法;
种不同的分法;
第二类:两组中人数都有女医生2人男医生3人.因为组与组之间无顺序,故共有![]() 种不同的分法.
种不同的分法.
因此,把10名医生分成两组,每组5人且每组都要有女医生的不同的分法共有![]() 种.
种.
若将这两组医生分派到两地去,并且每组选出正副组长两人,则共有
![]() 种不同方案
种不同方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中学生测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高一年级有男生
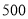 人,女生
人,女生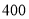 人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了
人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了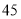 名学生的测评结果,并作出频数统计表如下:
名学生的测评结果,并作出频数统计表如下:等级
优秀
合格
尚待改进
频数
15
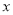
5
表一:男生
等级
优秀
合格
尚待改进
频数
15
3
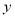
表二:女生
(1)从表二的非优秀学生中随机选取
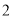 人交谈,求所选
人交谈,求所选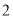 人中恰有
人中恰有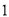 人测评等级为合格的概率;
人测评等级为合格的概率;(2)由表中统计数据填写
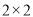 列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过
列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过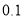 的前提下认为“测评结果优秀与性别有关”,参考数据与公示:
的前提下认为“测评结果优秀与性别有关”,参考数据与公示:  ,其中
,其中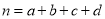
临界值表:
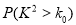
0.10
0.05
0.01
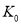
2.70
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
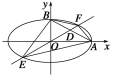
(1)若
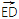 =6
=6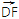 ,求k的值;
,求k的值;(2)求四边形AEBF面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
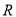 的函数
的函数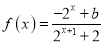 是奇函数.
是奇函数.(1)求
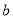 的值;
的值;(2)判断函数
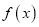 的单调性,并用定义证明;
的单调性,并用定义证明;(3)当
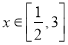 时,
时, 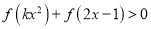 恒成立,求实数
恒成立,求实数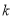 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
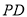 垂直于以
垂直于以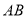 为直径的圆
为直径的圆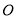 所在平面,点
所在平面,点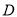 在线段
在线段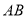 上,点
上,点 为圆
为圆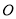 上一点,且
上一点,且

(Ⅰ) 求证:
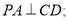
(Ⅱ) 求二面角
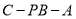 余弦值.
余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
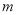 为何值时,
为何值时, 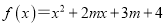 .①有且仅有一个零点;②有两个零点且均比-1大;
.①有且仅有一个零点;②有两个零点且均比-1大;(2)若函数
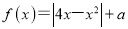 有4个零点,求实数
有4个零点,求实数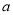 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
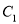 的中心为原点
的中心为原点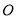 ,离心率
,离心率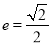 ,其中一个焦点的坐标为
,其中一个焦点的坐标为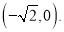
(Ⅰ)求椭圆
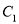 的标准方程;
的标准方程;(Ⅱ)当点
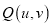 在椭圆
在椭圆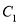 上运动时,设动点
上运动时,设动点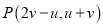 的运动轨迹为
的运动轨迹为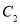 若点
若点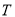 满足:
满足: 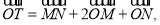 其中
其中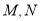 是
是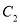 上的点.直线
上的点.直线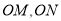 的斜率之积为
的斜率之积为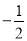 ,试说明:是否存在两个定点
,试说明:是否存在两个定点 ,使得
,使得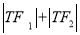 为定值?若存在,求
为定值?若存在,求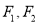 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
相关试题

