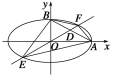
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
参考答案:
【答案】见解析
【解析】
解 (1)依题意得椭圆的方程为![]() +y2=1,直线AB,EF的方程分别为x+2y=2,y=kx(k>0).如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=
+y2=1,直线AB,EF的方程分别为x+2y=2,y=kx(k>0).如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=![]() .①
.①
由![]() =6
=6![]() 知x0-x1=6(x2-x0),
知x0-x1=6(x2-x0),
得x0=![]() (6x2+x1)=
(6x2+x1)=![]() x2=
x2=![]() ;
;
由D在AB上知x0+2kx0=2,
得x0=![]() .
.
所以![]() =
=![]() ,
,
化简得24k2-25k+6=0,
解得k=![]() 或k=
或k=![]() .
.
(2)根据点到直线的距离公式和①式知,点E,F到AB的距离分别为
h1=![]() =
=![]() ,
,
h2=![]() =
=![]() .
.
又|AB|=![]() =
=![]() ,
,
所以四边形AEBF的面积为
S=![]() |AB|(h1+h2)
|AB|(h1+h2)
=![]() ·
·![]() ·
·![]()
=![]()
=2![]() ≤2
≤2![]() ,
,
当4k2=1(k>0),即当k=![]() 时,上式取等号.
时,上式取等号.
所以S的最大值为2![]() .
.
即四边形AEBF面积的最大值为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,已知
中,已知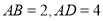 ,点
,点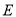 、
、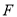 分别在
分别在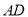 、
、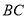 上,且
上,且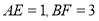 ,将四边形
,将四边形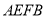 沿
沿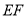 折起,使点
折起,使点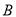 在平面
在平面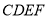 上的射影
上的射影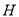 在直线
在直线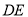 上.
上.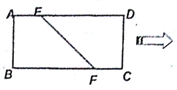
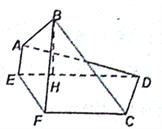
(I)求证:
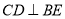 ;
;(II)求点
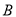 到平面
到平面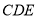 的距离;
的距离;(III)求直线
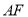 与平面
与平面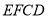 所成的正弦值.
所成的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在中学生测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高一年级有男生
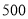 人,女生
人,女生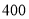 人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了
人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了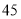 名学生的测评结果,并作出频数统计表如下:
名学生的测评结果,并作出频数统计表如下:等级
优秀
合格
尚待改进
频数
15
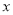
5
表一:男生
等级
优秀
合格
尚待改进
频数
15
3
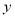
表二:女生
(1)从表二的非优秀学生中随机选取
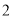 人交谈,求所选
人交谈,求所选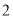 人中恰有
人中恰有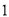 人测评等级为合格的概率;
人测评等级为合格的概率;(2)由表中统计数据填写
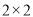 列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过
列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过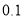 的前提下认为“测评结果优秀与性别有关”,参考数据与公示:
的前提下认为“测评结果优秀与性别有关”,参考数据与公示:  ,其中
,其中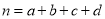
临界值表:
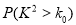
0.10
0.05
0.01
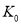
2.70
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
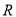 的函数
的函数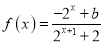 是奇函数.
是奇函数.(1)求
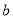 的值;
的值;(2)判断函数
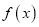 的单调性,并用定义证明;
的单调性,并用定义证明;(3)当
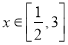 时,
时, 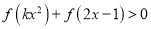 恒成立,求实数
恒成立,求实数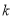 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
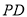 垂直于以
垂直于以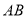 为直径的圆
为直径的圆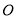 所在平面,点
所在平面,点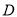 在线段
在线段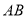 上,点
上,点 为圆
为圆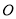 上一点,且
上一点,且

(Ⅰ) 求证:
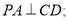
(Ⅱ) 求二面角
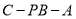 余弦值.
余弦值.
相关试题

