【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,离心率
,离心率![]() ,其中一个焦点的坐标为
,其中一个焦点的坐标为![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当点![]() 在椭圆
在椭圆![]() 上运动时,设动点
上运动时,设动点![]() 的运动轨迹为
的运动轨迹为![]() 若点
若点![]() 满足:
满足: ![]() 其中
其中![]() 是
是![]() 上的点.直线
上的点.直线![]() 的斜率之积为
的斜率之积为![]() ,试说明:是否存在两个定点
,试说明:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
参考答案:
【答案】(Ⅰ) ![]() (Ⅱ)详见解析.
(Ⅱ)详见解析.
【解析】试题分析: (Ⅰ)根据离心率和焦点坐标以及![]() 求出椭圆的标准方程;(Ⅱ)由于点
求出椭圆的标准方程;(Ⅱ)由于点![]() 在曲线
在曲线![]() 上运动时,动点
上运动时,动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ,通过
,通过![]() 可建立点T和点M,N坐标之间的关系式,通过直线
可建立点T和点M,N坐标之间的关系式,通过直线![]() 的斜率之积为定值,又得到另外一个关系式,且点M,N的坐标满足椭圆的方程,均为二次,因此给两等式分别平方,再对应系数比为1:2,相加即可得到关于x,y的方程,即点T的轨迹为椭圆,两个定点为焦点.
的斜率之积为定值,又得到另外一个关系式,且点M,N的坐标满足椭圆的方程,均为二次,因此给两等式分别平方,再对应系数比为1:2,相加即可得到关于x,y的方程,即点T的轨迹为椭圆,两个定点为焦点.
试题解析:(Ⅰ)由题意知, ![]() 所以
所以![]() 所以
所以![]()
故椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设![]() 则
则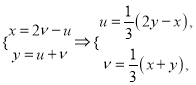
因为点![]() 在椭圆
在椭圆![]() 上运动,所以
上运动,所以![]()
故动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
由![]() 得
得
![]()
![]()
设![]() 分别为直线
分别为直线![]() 的斜率,由已知条件知
的斜率,由已知条件知![]() ,所以
,所以![]()
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]()
故![]()
![]()
从而知![]() 点是椭圆
点是椭圆![]() 上的点,所以,存在两个定点
上的点,所以,存在两个定点![]() 且为椭圆
且为椭圆![]() 的两个焦点,使得
的两个焦点,使得![]() 为定值.其坐标分别为
为定值.其坐标分别为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
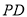 垂直于以
垂直于以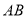 为直径的圆
为直径的圆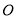 所在平面,点
所在平面,点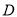 在线段
在线段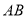 上,点
上,点 为圆
为圆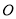 上一点,且
上一点,且

(Ⅰ) 求证:
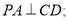
(Ⅱ) 求二面角
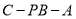 余弦值.
余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
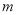 为何值时,
为何值时, 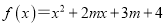 .①有且仅有一个零点;②有两个零点且均比-1大;
.①有且仅有一个零点;②有两个零点且均比-1大;(2)若函数
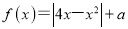 有4个零点,求实数
有4个零点,求实数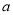 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:人们对声音有不同的感觉,这与它的强度有关系.声音的强度
 用瓦/米2 (
用瓦/米2 (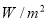 )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平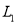 表示,它们满足以下公式:
表示,它们满足以下公式: 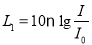 (单位为分贝,
(单位为分贝, 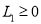 ,其中
,其中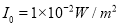 ,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:(1)树叶沙沙声的强度是
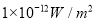 ,耳语的强度是
,耳语的强度是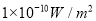 ,恬静的无线电广播的强度是
,恬静的无线电广播的强度是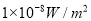 ,试分别求出它们的强度水平;
,试分别求出它们的强度水平;(2)某一新建的安静小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,试求声音强度
 的范围为多少?
的范围为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用
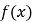 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(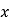 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),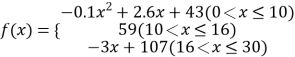 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 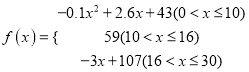 .
.(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
相关试题

