【题目】已知函数f(x)=sin(ωx+φ)﹣b(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是 ![]() ,若将f(x)的图象先向右平移
,若将f(x)的图象先向右平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位,所得函数g(x)为奇函数.
个单位,所得函数g(x)为奇函数.
(1)求f(x)的解析式;
(2)求f(x)的对称轴及单调区间;
(3)若对任意x∈[0, ![]() ],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:∵ ![]() ,∴ω=2∴f(x)=sin(2x+φ)﹣b.
,∴ω=2∴f(x)=sin(2x+φ)﹣b.
又 ![]() 为奇函数,且0<φ<π,则
为奇函数,且0<φ<π,则 ![]() ,
, ![]() ,故
,故 ![]()
(2)解:令2x+ ![]() =kπ+
=kπ+ ![]() ,求得
,求得 ![]() ,k∈Z,可得f(x)的图象的对称轴为
,k∈Z,可得f(x)的图象的对称轴为 ![]() ,k∈Z.
,k∈Z.
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函数的增区间为
,可得函数的增区间为 ![]() .
.
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ+
,求得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函数的减区间为
,可得函数的减区间为 ![]()
(3)解:由于 ![]() ,故
,故 ![]() ,∵f2(x)﹣(2+m)f(x)+2+m≤0恒成立,
,∵f2(x)﹣(2+m)f(x)+2+m≤0恒成立,
整理可得 ![]() .
.
由 ![]() ,得:
,得: ![]() ,故
,故 ![]() ,
,
即m取值范围是 ![]()
【解析】(1)利用正弦函数的周期性、奇偶性,求得ω和φ的值,可得f(x)的解析式.(2)利用正弦函数的单调性求得函数f(x)的单调区间.(3)利用正弦函数的定义域和值域,函数的恒成立问题,求得m的范围.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列命题的否定,并判断其真假:
(1)p:末位数字为9的整数能被3整除;
(2)p:有的素数是偶数;
(3)p:至少有一个实数x,使x2+1=0;
(4)p:x,y∈R,x2+y2+2x-4y+5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:任意两个等边三角形都是相似的.
①它的否定是_________________________________________________________;
②否命题是_____________________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
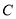 的极坐标方程为
的极坐标方程为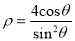 ,直线
,直线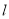 的参数方程为
的参数方程为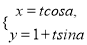 (
(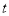 为参数,
为参数, 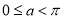 ).
).(Ⅰ)把曲线
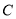 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线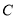 的形状;
的形状;(Ⅱ)若直线
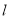 经过点
经过点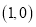 ,求直线
,求直线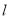 被曲线
被曲线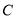 截得的线段
截得的线段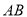 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinx+cosx=1,则(sinx)2018+(cosx)2018= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各命题作为原命题,分别写出它们的逆命题、否命题和逆否命题.
(1)若α=β,则sin α=sin β;
(2)若对角线相等,则梯形为等腰梯形;
(3)已知a,b,c,d都是实数,若a=b,c=d,则a+c=b+d.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则

 的最大值为 .
的最大值为 . 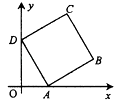
相关试题

