【题目】把下列各命题作为原命题,分别写出它们的逆命题、否命题和逆否命题.
(1)若α=β,则sin α=sin β;
(2)若对角线相等,则梯形为等腰梯形;
(3)已知a,b,c,d都是实数,若a=b,c=d,则a+c=b+d.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】试题分析:原命题是“若![]() 则
则![]() ”,逆命题是“若
”,逆命题是“若![]() 则
则![]() ”,否命题是“若
”,否命题是“若![]() 则
则![]() ”,逆否命题是“若
”,逆否命题是“若![]() 则
则![]() ”,互为逆否命题的命题是同真同假.
”,互为逆否命题的命题是同真同假.
(1)由任意角的定义即可判断真假;
(2)对角线相等未必是梯形;
(3)若a=b,c=d,必有a+c=b+d,反之不成立.
试题解析:
(1)逆命题:若sin α=sin β,则α=β;
否命题:若α≠β,则sin α≠sin β;
逆否命题:若sin α≠sin β,则α≠β.
(2)逆命题:若梯形为等腰梯形,则它的对角线相等;否命题:若梯形的对角线不相等,则梯形不是等腰梯形;
逆否命题:若梯形不是等腰梯形,则它的对角线不相等.
(3)逆命题:已知a,b,c,d都是实数,若a+c=b+d,则a=b,c=d;
否定题:已知a,b,c,d都是实数,若a≠b或c≠d,则a+c≠b+d;
逆否命题:已知a,b,c,d都是实数,若a+c≠b+d,则a≠b或c≠d.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
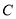 的极坐标方程为
的极坐标方程为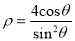 ,直线
,直线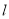 的参数方程为
的参数方程为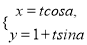 (
(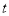 为参数,
为参数, 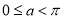 ).
).(Ⅰ)把曲线
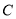 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线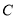 的形状;
的形状;(Ⅱ)若直线
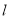 经过点
经过点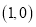 ,求直线
,求直线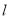 被曲线
被曲线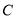 截得的线段
截得的线段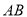 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)﹣b(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是
 ,若将f(x)的图象先向右平移
,若将f(x)的图象先向右平移  个单位,再向上平移
个单位,再向上平移 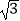 个单位,所得函数g(x)为奇函数.
个单位,所得函数g(x)为奇函数.
(1)求f(x)的解析式;
(2)求f(x)的对称轴及单调区间;
(3)若对任意x∈[0, ],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinx+cosx=1,则(sinx)2018+(cosx)2018= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则

 的最大值为 .
的最大值为 . 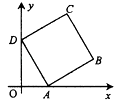
-
科目: 来源: 题型:
查看答案和解析>>【题目】设两个非零向量
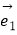 和
和  不共线.
不共线.
(1)如果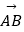 =
= 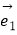 +
+  ,
, 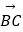 =2
=2 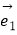 +8
+8  ,
, 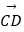 =3
=3 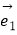 ﹣3
﹣3  ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;
(2)若|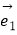 |=2,|
|=2,|  |=3,
|=3, 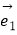 与
与  的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m 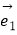 +
+  与
与 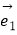 ﹣
﹣  垂直?并说明理由.
垂直?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间
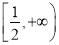 上为增函数”的________________.
上为增函数”的________________.
相关试题

