【题目】如图,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一点P在平面ABCD内的射影Q恰在边AD上, PA=AD=2 BC=2,CD=.
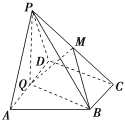
(1)若平面PQB⊥平面PAD,求证:Q为线段AD中点;
(2)在(1)的条件下,若M在线段PC上,且PA∥平面BMQ,求点M到平面PAB的距离.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】(1)证明:∵P在平面ABCD内的射影Q恰在边AD上,
∴PQ⊥平面ABCD,
∵BQ![]() 平面ABCD,∴PQ⊥BQ,(2分)
平面ABCD,∴PQ⊥BQ,(2分)
∵PQB⊥平面PAD,且平面PQB∩平面PAD =PQ,
∴BQ⊥平面PAD.
∵AD![]() 平面PAD,∴BQ⊥AD.(4分)
平面PAD,∴BQ⊥AD.(4分)
∵∠ADC=90°,∴CD∥BQ,
又AD∥BC,∴四边形BCDQ为平行四边形,
∴BC=QD=1,AQ=AD-QD=2-1=1,
∴AQ=QD,即Q为线段AD中点.(6分)
(2)连接AC与BQ交于点N,则N为AC中点,连接![]() ,
,
∵PA∥平面BMQ,∴PA∥MN,
∴M为PC中点,(8分)
∴点M到平面PAB的距离是点C到平面PAB的距离的![]() ,
,
在三棱锥![]() 中,高
中,高![]() ,底面积为
,底面积为![]() ,
,
∴三棱锥![]() 的体积
的体积![]() ,(10分)
,(10分)
又△PAB中,PA=AB=2,PB=![]() ,
,
∴△PAB的面积为![]() .
.
设点M到平面PAB的距离为d,由![]() 可得
可得![]() ,则
,则![]() ,
,
∴点M到平面PAB的距离为![]() .(12分)
.(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣2或3<x≤4},B={x|x2﹣2x﹣15≤0}.求:
(1)UA;
(2)A∪B;
(3)若C={x|x>a},且B∩C=B,求a的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x≤256,且log2x≥
 .
.
(1)求x的取值范围;
(2)求函数f(x)=log2( )log2(
)log2(  )的最大值和最小值.
)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

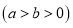 的左、右焦点分别为
的左、右焦点分别为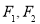 ,设点
,设点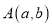 ,且
,且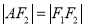 =2.
=2.(1)求椭圆C的方程;
(2)已知四边形MNPQ的四个顶点均在曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0).判断四边形MNPQ两条对角线的交点是否为定点?若是,求出定点坐标;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)讨论函数
 极值点的个数,并说明理由;
极值点的个数,并说明理由;(2)若
 ,
,  恒成立,求
恒成立,求 的最大整数值.
的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一企业从某条生产线上随机抽取30件产品,测量这些产品的某项技术指标值
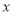 ,得到如下的频数分布表:
,得到如下的频数分布表: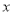
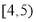
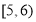
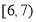
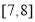
频数
2
6
18
4
(I)估计该技术指标值的平均数;(用各组区间中点值作代表)
(II) 若
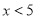 或
或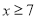 ,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;
,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;(III)生产一件产品,若是合格品可盈利80元,不合格品则亏损10元,在(II)的前提下,从该生产线生产的产品中任取出两件,记
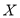 为两件产品的总利润,求随机变量X的分布列和期望.
为两件产品的总利润,求随机变量X的分布列和期望.
相关试题

