【题目】已知全集U=R,集合A={x|x<﹣2或3<x≤4},B={x|x2﹣2x﹣15≤0}.求:
(1)UA;
(2)A∪B;
(3)若C={x|x>a},且B∩C=B,求a的范围.
参考答案:
【答案】
(1)解:∵全集U=R,集合A={x|x<﹣2或3<x≤4},
∴UA={x|﹣2≤x≤3或x>4}
(2)解:由集合B中的不等式变形得:(x﹣5)(x+3)≤0,
解得:﹣3≤x≤5,即B={x|﹣3≤x≤5},
则A∪B={x|x≤5}
(3)解:∵B∩C=B,∴BC,
∵B={x|﹣3≤x≤5},C={x|x>a},
∴a<﹣3.
【解析】(1)由全集R及集合A,求出A的补集即可;(2)由A与B,求出两集合的并集即可;(3)根据B∩C=B,得到B为C的子集,由B与C求出a的范围即可.
【考点精析】认真审题,首先需要了解集合的并集运算(并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立),还要掌握集合的交集运算(交集的性质:(1)A∩B
B,反之也成立),还要掌握集合的交集运算(交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立)的相关知识才是答题的关键.
B,反之也成立)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,且当x≥0时,
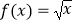 ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在
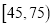 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差
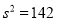 ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值 服从正态分布
服从正态分布 ,其中
,其中 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数 (注:求
(注:求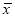 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表), 近似为样本方差
近似为样本方差 ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)(2)由以上统计数据完成下面
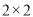 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
附注:
参考数据:
 ,
,参考公式:
 ,
,  ,
,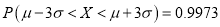 .
.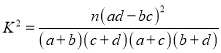

0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
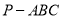 中,
中, 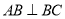 ,
,  ,
, 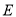 为
为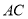 的中点.
的中点.(1)求证:
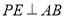 ;
;(2)设平面
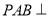 平面
平面 ,
, 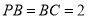 ,
, 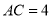 ,求二面角
,求二面角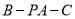 的平面角的正弦值.
的平面角的正弦值.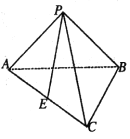
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x≤256,且log2x≥
 .
.
(1)求x的取值范围;
(2)求函数f(x)=log2( )log2(
)log2(  )的最大值和最小值.
)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一点P在平面ABCD内的射影Q恰在边AD上, PA=AD=2 BC=2,CD=.
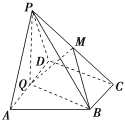
(1)若平面PQB⊥平面PAD,求证:Q为线段AD中点;
(2)在(1)的条件下,若M在线段PC上,且PA∥平面BMQ,求点M到平面PAB的距离.
相关试题

