【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
参考答案:
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意可知,共有25种结果,一次列出所有可能的结果即可;
(2)结合题意和(1)中列出的结果可得事件“取出卡片号码之和不小于7 或小于5”的概率是![]() .
.
试题解析:
(1)所有可能结果数为:25.
所有可能结果为:(1,1)(1,2)(1,3)(1,4)(1,5)(2,1)(2,2)(2,3)
(2,4)(2,5)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,1)(4,2)
(4,3)(4,4)(4,5)(5,1)(5,2)(5,3)(5,4)(5,5).
(2)记![]() “取出卡片号码之和小于7”,事件
“取出卡片号码之和小于7”,事件![]() 的频数为10,则
的频数为10,则![]() ,
,
记![]() “取出卡片号码之和小于5”,事件
“取出卡片号码之和小于5”,事件![]() 的频率为6,则
的频率为6,则![]() ,
,
∴事件“取出卡片号码之和不小于7 或小于5”的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
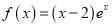 .
.(1)求
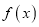 在
在 上的最小值
上的最小值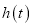 ;
;(2)若存在两个不同的实数
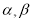 ,使得
,使得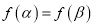 ,求证:
,求证: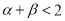 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的一种产品的广告费用
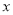 (单位:万元)与销售额
(单位:万元)与销售额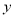 (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:广告费用
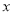
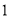
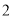
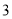
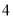
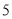
销售额
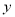
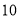
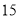

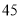
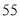
(1)根据上述数据,求出销售额
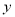 (万元)关于广告费用
(万元)关于广告费用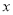 (万元)的线性回归方程;
(万元)的线性回归方程;(2)如果企业要求该产品的销售额不少于
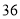 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?(参考数值:
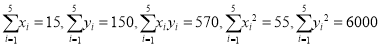 .
.回归直线的斜率和截距的最小二乘法估计公式分别为:
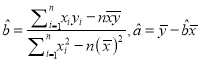 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某科研小组研究发现:一棵水蜜桃树的产量
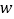 (单位:百千克)与肥料费用
(单位:百千克)与肥料费用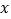 (单位:百元)满足如下关系:
(单位:百元)满足如下关系: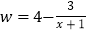 ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)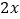 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为 (单位:百元).
(单位:百元).(1)求利润函数
 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表
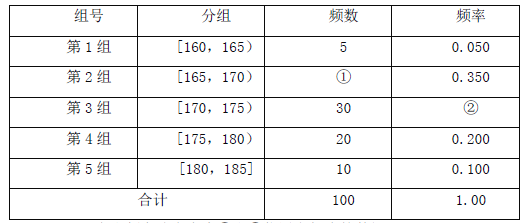
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5 组中用分层抽样的方法抽取6 名学生进行体能测试,求第3,4,5 组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6 名学生中随机抽取2 名学生进行引体向上测试,求第4 组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂每日生产某种产品
 吨,当日生产的产品当日销售完毕,产品价格随产品产量而变化,当
吨,当日生产的产品当日销售完毕,产品价格随产品产量而变化,当 时,每日的销售额
时,每日的销售额 (单位:万元)与当日的产量
(单位:万元)与当日的产量 满足
满足 ,当日产量超过
,当日产量超过 吨时,销售额只能保持日产量
吨时,销售额只能保持日产量 吨时的状况.已知日产量为
吨时的状况.已知日产量为 吨时销售额为
吨时销售额为 万元,日产量为
万元,日产量为 吨时销售额为
吨时销售额为 万元.
万元.(1)把每日销售额
 表示为日产量
表示为日产量 的函数;
的函数;(2)若每日的生产成本
 (单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.(注:计算时取
(单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.(注:计算时取 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学家里订了一份报纸,送报人每天都在早上6 : 207 : 40之间将报纸送达,该同学需要早上7 : 008 : 00之间出发上学,则这位同学在离开家之前能拿到报纸的概率为 ( )
A.
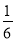 B.
B. 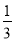 C.
C. 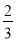 D.
D. 
相关试题

