【题目】高考数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.”某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大;
(3)所得分数ξ的数学期望.
参考答案:
【答案】
(1)解:得分为50分,10道题必须全做对.
在其余的四道题中,有两道题答对的概率为 ![]() ,有一道题答对的概率为
,有一道题答对的概率为 ![]() ,还有一道答对的概率为
,还有一道答对的概率为 ![]() ,所以得分为5(0分)的概率为:P=
,所以得分为5(0分)的概率为:P= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
(2)解:依题意,该考生得分的范围为{30,35,40,45,50}.
得分为30分表示只做对了6道题,其余各题都做错,所以概率为:P1= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
同样可以求得得分为35分的概率为:P2= ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
得分为40分的概率为:P3= ![]() ; 得分为4(5分)的概率为:P4=
; 得分为4(5分)的概率为:P4= ![]() ;
;
得分为50分的概率为:P5= ![]() .
.
所以得35分或得40分的可能性最大;
(3)解:由(2)可知ξ的分布列为:
ξ | 30 | 35 | 40 | 45 | 50 |
P |
|
|
|
|
|
∴Eξ=30× ![]() +35×
+35× ![]() +40×
+40× ![]() +45×
+45× ![]() +50×
+50× ![]() =
= ![]()
【解析】(1)根据题意,该考生10道题全答对即另四道题也全答对,根据相互独立事件概率的乘法公式,计算可得答案.(2)该考生选择题得分的可能取值有:30,35,40,45,50共五种.设选对一道“可判断2个选项是错误的”题目为事件A,“可判断1个选项是错误的”该题选对为事件B,“不能理解题意的”该题选对为事件C.得分为30,表示只做对有把握的那4道题,其余各题都做错;得分为35时,表示做对有把握的那4道题和另外四题中的一题;得分为40时,表示做对有把握的那4道题和另外四题中的二题;得分为45时,表示做对有把握的那4道题和另外四题中的三题;得分为50时,表示10题全部做对,做出概率.(3)由题意知变量的可能取值分别是30,35,40,45,50,根据第二问做出的结果,写出离散型随机变量的分布列,根据期望的定义,即可求出期望
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为
 (
( ,且
,且 );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )A. 每场比赛第一名得分
 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年3月山东省高考改革实施方案发布:2020年夏季高考开始全省高考考生总成绩将由语文、数学、外语三门统一高考成绩和学生自主选择的普通高中学业水平等级性考试科目的成绩共同构成.省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.右面是根据样本的调查结果绘制的等高条形图.

(Ⅰ)请根据已知条件与等高条形图完成下面的
 列联表:
列联表:赞成
不赞成
合计
城镇居民
农村居民
合计
(Ⅱ)试判断我们是否有95%的把握认为“赞成高考改革方案与城乡户口有关”?.
【附】
 ,其中
,其中 .
.
0.150
0.100
0.050
0.005
0.001

2.072
2.706
3.841
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
, 对任意的
对任意的 ,恒有
,恒有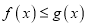 成立.
成立.(1)如果
 为奇函数,求
为奇函数,求 满足的条件.
满足的条件.(2)在(1)中条件下,若
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数);以原点
为参数);以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;(Ⅱ)若把曲线
 各点的横坐标伸长到原来的
各点的横坐标伸长到原来的 倍,纵坐标变为原来的
倍,纵坐标变为原来的 ,得到曲线
,得到曲线 ,求曲线
,求曲线 的方程;
的方程;(Ⅲ)设
 为曲线
为曲线 上的动点,求点
上的动点,求点 到曲线
到曲线 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
 DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC=  AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB. 
(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数  和
和 的图象如图
的图象如图

给出下列四个命题:
①方程
 有且仅有
有且仅有 个根;②方程
个根;②方程 有且仅有
有且仅有 个根;
个根;③方程
 有且仅有
有且仅有 个根;④方程
个根;④方程 有且仅有
有且仅有 个根;
个根;其中正确命题的序号是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
相关试题

