【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
参考答案:
【答案】C
【解析】若每场比赛第一名得分![]() 为4,则甲最后得分最高为
为4,则甲最后得分最高为![]() ,不合题意; 三人总分为
,不合题意; 三人总分为![]() ,每场总分数为
,每场总分数为![]() 分,所以
分,所以![]() ,因此 甲比赛名次为5个第一,一个第三;而乙比赛名次有1个第一,所以丙没有一场比赛获得第一名,因此选C.即乙比赛名次为1个第一,4个第三,1个第二.
,因此 甲比赛名次为5个第一,一个第三;而乙比赛名次有1个第一,所以丙没有一场比赛获得第一名,因此选C.即乙比赛名次为1个第一,4个第三,1个第二.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数fn(x)=xn+bx+c(n∈N* , b,c∈R)
(Ⅰ)设n≥2,b=1,c=﹣1,证明:fn(x)在区间(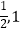 )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)设n=2,若对任意x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
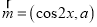 ,
, 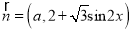 ,且函数
,且函数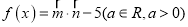 .
.(Ⅰ)当函数
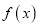 在
在 上的最大值为3时,求
上的最大值为3时,求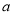 的值;
的值;(Ⅱ)在(Ⅰ)的条件下,若对任意的
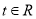 ,函数
,函数 ,
, 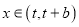 的图像与直线
的图像与直线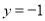 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定 的值.并求函数
的值.并求函数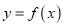 在
在 上的单调递减区间.
上的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下三个命题中:
①设有一个回归方程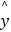 =2﹣3x,变量x增加一个单位时,y平均增加3个单位;
=2﹣3x,变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】各项均为非负整数的数列
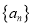 同时满足下列条件:
同时满足下列条件:①
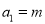
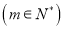 ;②
;②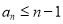
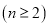 ;③
;③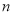 是
是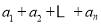 的因数(
的因数(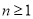 ).
).(Ⅰ)当
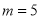 时,写出数列
时,写出数列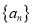 的前五项;
的前五项; (Ⅱ)若数列
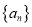 的前三项互不相等,且
的前三项互不相等,且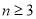 时,
时, 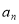 为常数,求
为常数,求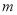 的值;
的值;(Ⅲ)求证:对任意正整数
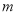 ,存在正整数
,存在正整数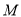 ,使得
,使得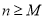 时,
时, 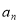 为常数.
为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
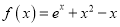 ,
, 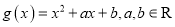 .
.(Ⅰ)当
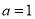 时,求函数
时,求函数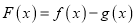 的单调区间;
的单调区间;(Ⅱ)若曲线
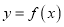 在点
在点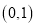 处的切线
处的切线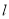 与曲线
与曲线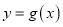 切于点
切于点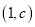 ,求
,求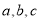 的值;
的值;(Ⅲ)若
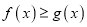 恒成立,求
恒成立,求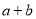 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
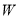 :
: 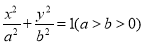 的上下顶点分别为
的上下顶点分别为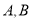 ,且点
,且点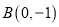 .
. 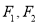 分别为椭圆
分别为椭圆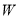 的左、右焦点,且
的左、右焦点,且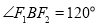 .
. (Ⅰ)求椭圆
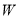 的标准方程;
的标准方程;(Ⅱ)点
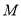 是椭圆上异于
是椭圆上异于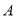 ,
, 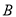 的任意一点,过点
的任意一点,过点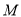 作
作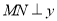 轴于
轴于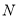 ,
, 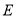 为线段
为线段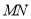
的中点.直线
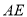 与直线
与直线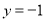 交于点
交于点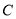 ,
, 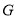 为线段
为线段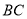 的中点,
的中点, 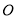 为坐标原点.求
为坐标原点.求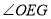 的大小.
的大小.
相关试题

