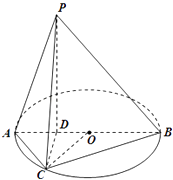
【题目】如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= ![]() DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC= ![]() AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB. 
(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值.
参考答案:
【答案】
(1)证明:连接OC,由AD= ![]() BD知,点D为AO的中点,
BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,
∵ ![]() AC=BC,∴∠CAB=60°,
AC=BC,∴∠CAB=60°,
∴△ACO为等边三角形,∴CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA平面PAB,
∴PA⊥CD.
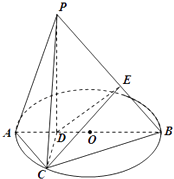
(2)解:过点D作DE⊥PB,垂足为E,连接CE,
由(1)知CD⊥平面PAB,又PB平面PAB,
∴CD⊥PB,又DE∩CD=D,
∴PB⊥平面CDE,又CE平面CDE,
∴CE⊥PB,
∴∠DEC为二面角C﹣PB﹣A的平面角.
由(1)可知CD= ![]() ,PD=BD=3,
,PD=BD=3,
∴PB=3 ![]() ,则DE=
,则DE= ![]() =
= ![]() ,
,
∴在Rt△CDE中,tan∠DEC= ![]() =
= ![]() ,
,
∴cos∠DEC= ![]() ,即二面角C﹣PB﹣A的余弦值为
,即二面角C﹣PB﹣A的余弦值为 ![]()
【解析】(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直线面垂直,再由线面垂直线线垂直;(2)通过作出二面角的平面角,证明符合定义,再在三角形中求解.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
, 对任意的
对任意的 ,恒有
,恒有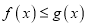 成立.
成立.(1)如果
 为奇函数,求
为奇函数,求 满足的条件.
满足的条件.(2)在(1)中条件下,若
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】高考数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.”某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大;
(3)所得分数ξ的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数);以原点
为参数);以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;(Ⅱ)若把曲线
 各点的横坐标伸长到原来的
各点的横坐标伸长到原来的 倍,纵坐标变为原来的
倍,纵坐标变为原来的 ,得到曲线
,得到曲线 ,求曲线
,求曲线 的方程;
的方程;(Ⅲ)设
 为曲线
为曲线 上的动点,求点
上的动点,求点 到曲线
到曲线 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数  和
和 的图象如图
的图象如图

给出下列四个命题:
①方程
 有且仅有
有且仅有 个根;②方程
个根;②方程 有且仅有
有且仅有 个根;
个根;③方程
 有且仅有
有且仅有 个根;④方程
个根;④方程 有且仅有
有且仅有 个根;
个根;其中正确命题的序号是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为打入国际市场,决定从
 、
、 两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)年固定成本
每件产品成本
每件产品销售价
每年最多可生产的件数
A产品
20

10
200
B产品
40
8
18
120
其中年固定成本与年生产的件数无关,
 是待定常数,其值由生产
是待定常数,其值由生产 产品的原材料决定,预计
产品的原材料决定,预计 ,另外,年销售
,另外,年销售 件B产品时需上交
件B产品时需上交 万美元的特别关税,假设生产出来的产品都能在当年销售出去.
万美元的特别关税,假设生产出来的产品都能在当年销售出去.(1)求该厂分别投资生产A、
 两种产品的年利润
两种产品的年利润 与生产相应产品的件数
与生产相应产品的件数 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;(2)如何投资才可获得最大年利润?请设计相关方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输出的
 ,则判断框内可以填入
,则判断框内可以填入
A.
 B.
B.  C.
C.  D.
D. 
相关试题

