【题目】如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ![]() ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O= ![]() .
. 
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
参考答案:
【答案】
(1)证明:连接OD,OE.
因为在等腰直角三角形ABC中,∠B=∠C=45°, ![]() ,CO=BO=3.
,CO=BO=3.
在△COD中, ![]() ,同理得
,同理得 ![]() .
.
因为 ![]() ,
, ![]() .
.
所以A′O2+OD2=A′D2,A′O2+OE2=A′E2.
所以∠A′OD=∠A′OE=90°
所以A′O⊥OD,A′O⊥OE,OD∩OE=O.
所以A′O⊥平面BCDE.
(2)方法一:
过点O作OF⊥CD的延长线于F,连接A′F
因为A′O⊥平面BCDE.
根据三垂线定理,有A′F⊥CD.
所以∠A′FO为二面角A′﹣CD﹣B的平面角.
在Rt△COF中, ![]() .
.
在Rt△A′OF中, ![]() =
= ![]() .
.
所以 ![]() .
.
所以二面角A′﹣CD﹣B的平面角的余弦值为 ![]() .
.

方法二:
取DE中点H,则OH⊥OB.
以O为坐标原点,OH、OB、OA′分别为x、y、z轴建立空间直角坐标系.
则O(0,0,0),A′(0,0, ![]() ),C(0,﹣3,0),D(1,﹣2,0)
),C(0,﹣3,0),D(1,﹣2,0) ![]() =(0,0,
=(0,0, ![]() )是平面BCDE的一个法向量.
)是平面BCDE的一个法向量.
设平面A′CD的法向量为n=(x,y,z) ![]() ,
, ![]() .
.
所以  ,令x=1,则y=﹣1,
,令x=1,则y=﹣1, ![]() .
.
所以 ![]() 是平面A′CD的一个法向量
是平面A′CD的一个法向量
设二面角A′﹣CD﹣B的平面角为θ,且 ![]()
所以 
所以二面角A′﹣CD﹣B的平面角的余弦值为 ![]()

【解析】(1)连接OD,OE.在等腰直角三角形ABC中,∠B=∠C=45°, ![]() ,AD=AE=
,AD=AE= ![]() ,CO=BO=3.分别在△COD与△OBE中,利用余弦定理可得OD,OE.利用勾股定理的逆定理可证明∠A′OD=∠A′OE=90°,再利用线面垂直的判定定理即可证明;(2)方法一:过点O作OF⊥CD的延长线于F,连接A′F.利用(1)可知:A′O⊥平面BCDE,根据三垂线定理得A′F⊥CD,所以∠A′FO为二面角A′﹣CD﹣B的平面角.在直角△OCF中,求出OF即可;方法二:取DE中点H,则OH⊥OB.以O为坐标原点,OH、OB、OA′分别为x、y、z轴建立空间直角坐标系.利用两个平面的法向量的夹角即可得到二面角.
,CO=BO=3.分别在△COD与△OBE中,利用余弦定理可得OD,OE.利用勾股定理的逆定理可证明∠A′OD=∠A′OE=90°,再利用线面垂直的判定定理即可证明;(2)方法一:过点O作OF⊥CD的延长线于F,连接A′F.利用(1)可知:A′O⊥平面BCDE,根据三垂线定理得A′F⊥CD,所以∠A′FO为二面角A′﹣CD﹣B的平面角.在直角△OCF中,求出OF即可;方法二:取DE中点H,则OH⊥OB.以O为坐标原点,OH、OB、OA′分别为x、y、z轴建立空间直角坐标系.利用两个平面的法向量的夹角即可得到二面角.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.(Ⅰ)求角
 的大小;
的大小;(Ⅱ)若
 ,
, ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”,其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,则该人第五天走的路程为( )
A. 6里B. 12里C. 24里D. 48里
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 已知a1=1,
 ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知六棱锥
 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, ,给出下列结论:
,给出下列结论:
①
 ;
;②直线
 平面
平面 ;
;③平面
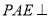 平面
平面 ;
;④异面直线
 与
与 所成角为
所成角为 ;
;⑤直线
 与平面
与平面 所成角的余弦值为
所成角的余弦值为 .
.其中正确的有_______(把所有正确的序号都填上)
相关试题

