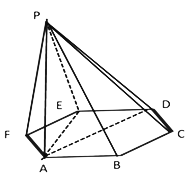
【题目】如图,已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①![]() ;
;
②直线![]() 平面
平面![]() ;
;
③平面![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的有_______(把所有正确的序号都填上)
参考答案:
【答案】①③④⑤
【解析】
设出几何体的边长,根据正六边形的性质,线面垂直的判定定理,线面平行的判定定理,面面垂直的判定定理,异面直线所成角,线面角有关知识,对五个结论逐一分析,由此得出正确结论的序号.
设正六边形长为![]() ,则
,则![]() .根据正六边形的几何性质可知
.根据正六边形的几何性质可知![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,故①正确.由于
,故①正确.由于![]() ,而
,而![]() ,所以直线
,所以直线![]() 平面
平面![]() 不正确,故②错误.易证得
不正确,故②错误.易证得![]() ,所以
,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,故③正确.由于
,故③正确.由于![]() ,所以
,所以![]() 是异面直线
是异面直线![]() 与
与![]() 所成角,在
所成角,在![]() 中,
中,![]() ,故
,故![]() ,也即异面直线
,也即异面直线![]() 与
与![]() 所成角为
所成角为![]() ,故④正确.连接
,故④正确.连接![]() ,则
,则![]() ,由①证明过程可知
,由①证明过程可知![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 是所求线面角,在三角形
是所求线面角,在三角形![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]() ,故⑤正确.综上所述,正确的序号为①③④⑤.
,故⑤正确.综上所述,正确的序号为①③④⑤.
-
科目: 来源: 题型:
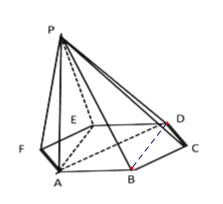
查看答案和解析>>【题目】如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,
 ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=  .
. 
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 已知a1=1,
 ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四棱锥
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, 分别是
分别是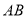 ,
, 的中点,
的中点, 与平面
与平面 所成的角的正切值是
所成的角的正切值是 ;
;
(1)求证:
 平面
平面 ;
;(2)求二面角
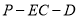 的正切值.
的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,其中
,其中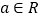 .
.(Ⅰ)当
 时,求函数
时,求函数 的极值;
的极值;(Ⅱ)当
 时,证明:函数
时,证明:函数 不可能存在两个零点.
不可能存在两个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某设计师设计的
 型饰品的平面图,其中支架
型饰品的平面图,其中支架 ,
, ,
, 两两成
两两成 ,
, ,
, ,且
,且 .现设计师在支架
.现设计师在支架 上装点普通珠宝,普通珠宝的价值为
上装点普通珠宝,普通珠宝的价值为 ,且
,且 与
与 长成正比,比例系数为
长成正比,比例系数为 (
( 为正常数);在
为正常数);在 区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为
区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为 ,且
,且 与
与 的面积成正比,比例系数为
的面积成正比,比例系数为 .设
.设 ,
, .
.
(1)求
 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;(2)求
 的最大值及相应的
的最大值及相应的 的值.
的值.
相关试题

