【题目】下列函数中,既是偶函数又在区间(﹣∞,0)上单调递增的是( )
A.f(x)= ![]()
B.f(x)=x2+1
C.f(x)=x
D.f(x)=2x
参考答案:
【答案】A
【解析】解:在A 中,f(x)= ![]() 是偶函数,在区间(﹣∞,0)上单调递增,故A正确;
是偶函数,在区间(﹣∞,0)上单调递增,故A正确;
在B中,f(x)=x2+1是偶函数,在区间(﹣∞,0)上单调递减,故B错误;
在C中,f(x)=x是奇函数,在(﹣∞,0)上是增函数,故C错误;
在D中,f(x)=2x是非奇非偶函数,在(﹣∞,0)上是增函数,故D错误.
故选:A.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的二次方程px2+(p﹣1)x+p+1=0有两个不相等的正根,且一根大于另一根的两倍,求p的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a≠0),记f[2](x)=f(f(x)),例:f(x)=x2+1,
则f[2](x)=(f(x))2+1=(x2+1)2+1;
(1)f(x)=x2﹣x,解关于x的方程f[2](x)=x;
(2)记△=(b﹣1)2﹣4ac,若f[2](x)=x有四个不相等的实数根,求△的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
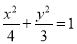 的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.(1)求该椭圆的离心率;
(2)设直线AB和AC分别与直线x=4交于点M,N,问:x轴上是否存在定点P使得MP⊥NP?若存在,求出点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
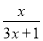 ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).(1)证明数列{
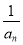 }是等差数列,并求出数列{an}的通项公式;
}是等差数列,并求出数列{an}的通项公式;(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油
 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
相关试题

