【题目】已知椭圆![]() 的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
(1)求该椭圆的离心率;
(2)设直线AB和AC分别与直线x=4交于点M,N,问:x轴上是否存在定点P使得MP⊥NP?若存在,求出点P的坐标;若不存在,说明理由.
参考答案:
【答案】(1)![]() (2)存在定点P(1,0)或P(7,0),
(2)存在定点P(1,0)或P(7,0),
【解析】试题分析:(1)由椭圆方程分别求出a,b,c的值,求出离心率;(2)假设在x轴上存在点p,设直线BC的方程为![]() ,B(x1,y1),C(x2,y2),
,B(x1,y1),C(x2,y2),
联立直线和椭圆方程,利用韦达定理求出![]() 的表达式,求出M,N的坐标,由MP⊥NP,求出P点的坐标,即得出定点。
的表达式,求出M,N的坐标,由MP⊥NP,求出P点的坐标,即得出定点。
试题解析: (1)由椭圆方程可得a=2,b=![]() ,从而椭圆的半焦距c=
,从而椭圆的半焦距c=![]() =1.
=1.
所以椭圆的离心率为e=![]() =
=![]() .
.
(2)依题意,直线BC的斜率不为0,
设其方程为x=ty+1.
将其代入![]() +
+![]() =1,整理得(4+3t2)y2+6ty-9=0.
=1,整理得(4+3t2)y2+6ty-9=0.
设B(x1,y1),C(x2,y2),
所以y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
易知直线AB的方程是y=![]() (x+2),
(x+2),
从而可得M(4,![]() ),同理可得N(4,
),同理可得N(4,![]() ).
).
假设x轴上存在定点P(p,0)使得MP⊥NP,则有![]() ·
·![]() =0.
=0.
所以(p-4)2+![]() =0.
=0.
将x1=ty1+1,x2=ty2+1代入上式,整理得
(p-4)2+![]() =0,
=0,
所以(p-4)2+![]() =0,
=0,
即(p-4)2-9=0,解得p=1或p=7.
所以x轴上存在定点P(1,0)或P(7,0),使得MP⊥NP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+1,a,b∈R,当x=﹣1时,函数f(x)取到最小值,且最小值为0;
(1)求f(x)解析式;
(2)关于x的方程f(x)=|x+1|﹣k+3恰有两个不相等的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的二次方程px2+(p﹣1)x+p+1=0有两个不相等的正根,且一根大于另一根的两倍,求p的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a≠0),记f[2](x)=f(f(x)),例:f(x)=x2+1,
则f[2](x)=(f(x))2+1=(x2+1)2+1;
(1)f(x)=x2﹣x,解关于x的方程f[2](x)=x;
(2)记△=(b﹣1)2﹣4ac,若f[2](x)=x有四个不相等的实数根,求△的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,既是偶函数又在区间(﹣∞,0)上单调递增的是( )
A.f(x)=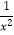
B.f(x)=x2+1
C.f(x)=x
D.f(x)=2x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
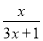 ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).(1)证明数列{
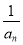 }是等差数列,并求出数列{an}的通项公式;
}是等差数列,并求出数列{an}的通项公式;(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
相关试题

